
【题目】综合与实践
问题情境
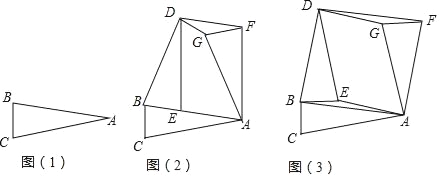
在综合实践课上,老师让同学们“以三角形的旋转”为主题进行数学活动,如图(1),在三角形纸片ABC中,AB=AC,∠B=∠C=α.
操作发现
(1)创新小组将图(1)中的△ABC以点B为旋转中心,逆时针旋转角度α,得到△DBE,再将△ABC以点A为旋转中心,顺时针旋转角度α,得到△AFG,连接DF,得到图(2),则四边形AFDE的形状是 .
(2)实践小组将图(1)中的△ABC以点B为旋转中心,逆时针逆转90°,得到△DBE,再将△ABC以点A为旋转中心,顺时针旋转90°,得到△AFG,连接DF、DG、AE,得到图(3),发现四边形AFDB为正方形,请你证明这个结论.
拓展探索
(3)请你在实践小组操作的基础上,再写出图(3)中的一个特殊四边形,并证明你的结论.
【答案】(1)平行四边形;(2)证明见解析(3)四边形AEDG是平行四边形.
【解析】试题分析:(1)由旋转的性质和旋转角度可求得DE∥AF,且DE=AF,可证明四边形AFDE为平行四边形;
(2)由旋转的性质和旋转角度可求得DE∥AF,且DE=AF,可证明四边形AFDE为平行四边形,再由旋转角是90°,即可得出结论;
(3)由旋转的性质和旋转角度判断出△ABE≌△DFG即可得出结论.
试题解析:
(1)证明:∵△DBE是由△ABC绕点B逆时针旋转90°得到的,△AFG是由△ABC绕点A顺时针旋转90°得到的.
∴DE=AC=AF,∠BAF=α,∠DBE=∠ABC=α,∠DEB=∠C=α,
∴∠DEB=∠BAF,
∴DE∥AF,
∵DE=AF,
∴四边形AFDE是平行四边形,
故答案为:平行四边形;
(2)证明:∵△DBE是由△ABC绕点B逆时针旋转90°得到的,△AFG是由△ABC绕点A顺时针旋转90°得到的,
∴∠DBA=∠FAB=90°,DB=AB=AF,
∴∠DBA+∠FAB=180°,
∴DB∥AF,
∵DB=AF,
∴四边形DBAF是平行四边形,
∵∠DBA=90°
∴平行四边形DBAF是正方形.
(3)四边形AEDG是平行四边形.
证明:∵四边形ABDF是正方形,
∴∠DFA=∠DBA=90°,AB=DF,
又∵∠DBE=∠AFG=α,
∴∠EBA=∠GFD.
在△ABE和△DFG中,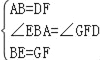 ,
,
∴△ABE≌△DFG,
∴AE=DG,
又∵DE=AG=AB,
∴四边形DEAG是平行四边形.


科目:初中数学 来源: 题型:
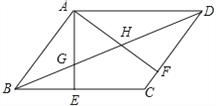
【题目】如图,在平行四边形ABCD中,AE⊥BC于E,AF⊥CD于F,BD与AE、AF交于G、H.
(1)求证:△ABE∽△ADF;
(2)若AG=AH,求证:四边形ABCD是菱形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】随着“一带一路”的进一歩推进,我国瓷器(“china”)更为“一带一路”沿践人民所推崇,一外国商户准这一商机,向我国一瓷器经销商咨询工艺品茶具,得到如下信息:
(1)每个茶壶的批发价比每个茶杯多120元;
(2)一套茶具包括一个茶壶与四个茶杯;
(3)4套茶具的批发价为1280元.
根据以上僖息:
(1)求每个茶壶与每个茶杯的批发价;
(2)若该商户购进茶杯的数量是茶壶数量的5倍还多18个,并且茶壶和茶杯的总数不超过320个,该商户计划将一半的茶具按每套500元成套销售,其余按每个茶壶300元,每个茶杯80元零售.没核商户购进茶壶m个.
①试用含m的关系式表示出该商户计划获取的利润;
②请帮助他设计一种获取利润最大的方案,并求出最大利润.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(本题满分10分)小明在一次高尔夫球的练习中,在点O处击球,其飞行路线满足抛物线![]() ,其中y(m)是球的飞行高度,
,其中y(m)是球的飞行高度, ![]() (m)是球飞出的水平距离,结果球离球洞的水平距离还有2m.
(m)是球飞出的水平距离,结果球离球洞的水平距离还有2m.
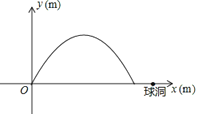
(1)求抛物线的顶点坐标及球飞行的最大水平距离;
(2)若小明第二次仍从点O处击球,球飞行的最大高度不变且刚好进洞,求球飞行的抛物线路线满足的函数表达式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,点P、Q分别是边长为4cm的等边三角形ABC的边AB、BC上的动点,点P从顶点A,点Q从顶点B同时出发,且它们的速度都为1cm/s.

(1)连接AQ、CP交于点M,则在P,Q运动的过程中,证明![]() ≌
≌![]() ;
;
(2)![]() 会发生变化吗?若变化,则说明理由,若不变,则求出它的度数;
会发生变化吗?若变化,则说明理由,若不变,则求出它的度数;
(3)P、Q运动几秒时,![]() 是直角三角形?
是直角三角形?
(4)如图2,若点P、Q在运动到终点后继续在射线AB、BC上运动,直线AQ、CP交点为M,则![]() 变化吗?若变化说明理由,若不变,则求出它的度数。
变化吗?若变化说明理由,若不变,则求出它的度数。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com