
 口算能手系列答案
口算能手系列答案科目:初中数学 来源: 题型:解答题
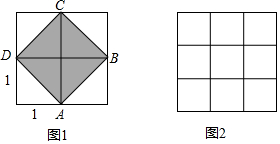 观察图1:每个小正方形的边长均是1,我们可以得到小正方形的面积为1.
观察图1:每个小正方形的边长均是1,我们可以得到小正方形的面积为1.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
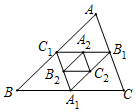 如图,已知△ABC的面积是1,A1、B1、C1分别是△ABC三边上的中点,△A1B1C1面积记为S1,A2、B2、C2分别是△A1B1C1三边上的中点,△A2B2C2的面积记为S2,以此类推,则△A4B4C4的面积S4=$\frac{1}{256}$.
如图,已知△ABC的面积是1,A1、B1、C1分别是△ABC三边上的中点,△A1B1C1面积记为S1,A2、B2、C2分别是△A1B1C1三边上的中点,△A2B2C2的面积记为S2,以此类推,则△A4B4C4的面积S4=$\frac{1}{256}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
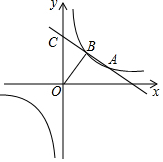 如图,一次函数y=kx+b(k<0)与反比例函数y=$\frac{m}{x}$的图象相交于A、B两点,一次函数的图象与y轴相交于点C,已知点A(4,1)
如图,一次函数y=kx+b(k<0)与反比例函数y=$\frac{m}{x}$的图象相交于A、B两点,一次函数的图象与y轴相交于点C,已知点A(4,1)查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
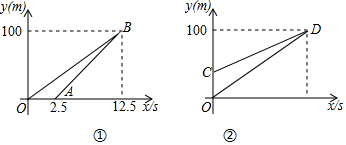
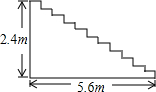 某宾馆在重新装修后,准备在大厅主楼梯上铺设某种红色地毯,已知这种地毯每平方米售价40元,主楼梯道宽2米,其侧面如图所示,则购买地毯至少需要640元.
某宾馆在重新装修后,准备在大厅主楼梯上铺设某种红色地毯,已知这种地毯每平方米售价40元,主楼梯道宽2米,其侧面如图所示,则购买地毯至少需要640元.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com