
【题目】某市从今年1月1日起调整居民用水价格,每吨水费上涨三分之一,小丽家去年12月的水费是15元,今年2月的水费是30元.已知今年2月的用水量比去年12月的用水量多5吨,求该市今年居民用水的价格?
【答案】解:设去年每吨水费为x元,则今年每吨水费为(1+ ![]() )x元,小丽家去年12月的用水量为
)x元,小丽家去年12月的用水量为 ![]() 吨,今年2月的用水量为(
吨,今年2月的用水量为( ![]() +5)吨, 根据题意得:(
+5)吨, 根据题意得:( ![]() +5)(1+
+5)(1+ ![]() )x=30,
)x=30,
解得:x=1.5,
经检验得:x=1.5是原方程的根,
∴(1+ ![]() )x=2.
)x=2.
答:该市今年居民用水的价格为2元/吨
【解析】设去年每吨水费为x元,则今年每吨水费为(1+ ![]() )x元,小丽家去年12月的用水量为
)x元,小丽家去年12月的用水量为 ![]() 吨,今年2月的用水量为(
吨,今年2月的用水量为( ![]() +5)吨,根据应缴水费=水费单价×用水量即可得出关于x的分式方程,解之经检验后即可得出x值,将其代入(1+
+5)吨,根据应缴水费=水费单价×用水量即可得出关于x的分式方程,解之经检验后即可得出x值,将其代入(1+ ![]() )x中即可得出结论.
)x中即可得出结论.
【考点精析】掌握分式方程的应用是解答本题的根本,需要知道列分式方程解应用题的步骤:审题、设未知数、找相等关系列方程、解方程并验根、写出答案(要有单位).


 全能测控期末小状元系列答案
全能测控期末小状元系列答案科目:初中数学 来源: 题型:
【题目】某工厂一周计划每日生产某产品100吨,由于工人实行轮休,每日上班人数不一定相等,实际每日生产量与计划量相比情况如下表(以计划量为标准,增加的吨数记为正数,减少的吨数记为负数)
星期 | 一 | 二 | 三 | 四 | 五 | 六 | 日 |
增减/吨 | ﹣1 | +3 | ﹣2 | +4 | +7 | ﹣5 | ﹣10 |
(1)生产量最多的一天比生产量最少的一天多生产多少吨?
(2)本周总生产量是多少吨?比原计划增加了还是减少了?增减数为多少吨?
(3)若本周总生产的产品全部由35辆货车一次性装载运输离开工厂,则平均每辆货车大约需装载多少吨?(结果精确到0.01吨)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,在平面直角坐标系xOy中,反比例函数y= ![]() 的图像与正比例函数y=kx(k≠0)的图像相交于横坐标为2的点A,平移直线OA,使它经过点B(3,0).
的图像与正比例函数y=kx(k≠0)的图像相交于横坐标为2的点A,平移直线OA,使它经过点B(3,0). 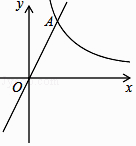
(1)求平移后直线的表达式;
(2)求OA平移后所得直线与双曲线的交点坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,点M、N是∠ABC与∠ACB三等分线的交点.若∠A=60°,则∠BMN的度数为( )

A. 45° B. 50° C. 60° D. 65°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在边长为1个单位长度的小正方形组成的网格中,给出了格点△ABC和△DEF(顶点为网格线的交点),以及过格点的直线l.
(1)将△ABC向右平移两个单位长度,再向下平移两个单位长度,画出平移后的三角形.
(2)画出△DEF关于直线l对称的三角形.
(3)填空:∠C+∠E= .

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD为正方形,若AB=4,E是AD边上一点(点E与点A、D不重合),BE的中垂线交AB于点M,交DC于点N,设AE=x,BM=y,则y与x的大致图象是( )

A. B.
B. C.
C. D.
D.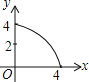
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知在平面直角坐标系中,一次函数y= ![]() x+3的图像与y轴交于点A,点M在正比例函数y=
x+3的图像与y轴交于点A,点M在正比例函数y= ![]() x的图像x>0的那部分上,且MO=MA(O为坐标原点).
x的图像x>0的那部分上,且MO=MA(O为坐标原点).
(1)求线段AM的长;
(2)若反比例函数y= ![]() 的图像经过点M关于y轴的对称点M′,求反比例函数解析式,并直接写出当x>0时,
的图像经过点M关于y轴的对称点M′,求反比例函数解析式,并直接写出当x>0时, ![]() x+3与
x+3与 ![]() 的大小关系.
的大小关系.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某单位举行“健康人生”徒步走活动,某人从起点体育村沿建设路到市生态园,再沿原路返回,设此人离开起点的路程s(千米)与走步时间t(小时)之间的函数关系如图所示,其中从起点到市生态园的平均速度是4千米/小时,用2小时,根据图像提供信息,解答下列问题. 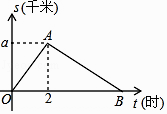
(1)求图中的a值.
(2)若在距离起点5千米处有一个地点C,此人从第一次经过点C到第二次经过点C,所用时间为1.75小时. ①求AB所在直线的函数解析式;
②请你直接回答,此人走完全程所用的时间.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com