
”¾ĢāÄæ”æ£Ø±¾ĢāĀś·Ö12·Ö£©æģ”¢ĀżĮ½³µ·Ö±š“ÓĻą¾ą480Ē§Ć×Ā·³ĢµÄ¼×”¢ŅŅĮ½µŲĶ¬Ź±³ö·¢£¬ŌČĖŁŠŠŹ»£¬ĻČĻąĻņ¶ųŠŠ£¬Ķ¾ÖŠĀż³µŅņ¹ŹĶ£Įō1Š”Ź±£¬Č»ŗóŅŌŌĖŁ¼ĢŠųĻņ¼×µŲŠŠŹ»£¬µ½“ļ¼×µŲŗóĶ£Ö¹ŠŠŹ»£»æģ³µµ½“ļŅŅµŲŗó£¬Į¢¼“°“ŌĀ·ŌĖŁ·µ»Ų¼×µŲ£Øæģ³µµōĶ·µÄŹ±¼äŗöĀŌ²»¼Ę£©£¬æģ”¢ĀżĮ½³µ¾ąŅŅµŲµÄĀ·³Ģ![]() £ØĒ§Ć×£©ÓėĖłÓĆŹ±¼ä
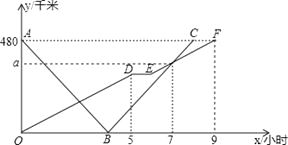
£ØĒ§Ć×£©ÓėĖłÓĆŹ±¼ä![]() £ØŠ”Ź±£©Ö®¼äµÄŗÆŹżĶ¼ĻóČēĶ¼£¬Ēė½įŗĻĶ¼ĻóŠÅĻ¢½ā“šĻĀĮŠĪŹĢā£ŗ
£ØŠ”Ź±£©Ö®¼äµÄŗÆŹżĶ¼ĻóČēĶ¼£¬Ēė½įŗĻĶ¼ĻóŠÅĻ¢½ā“šĻĀĮŠĪŹĢā£ŗ
£Ø1£©ĒóĀż³µµÄŠŠŹ»ĖŁ¶ČŗĶ![]() µÄÖµ£»
掙术
£Ø2£©Ēóæģ³µÓėĀż³µµŚŅ»“ĪĻąÓöŹ±£¬¾ąĄė¼×µŲµÄĀ·³ĢŹĒ¶ąÉŁĒ§Ć×£æ
£Ø3£©ĒóĮ½³µ³ö·¢ŗó¼øŠ”Ź±Ļą¾ąµÄĀ·³ĢĪŖ![]() Ē§Ć×£æ
Ē§Ć×£æ
”¾“š°ø”æ£Ø1£©60Ē§Ć×/Ź±,360;£Ø2£©320Ē§Ć×;£Ø3£©![]() ”¢
Ӣ![]() Ӣ
”¢![]() Š”Ź±
Š”Ź±
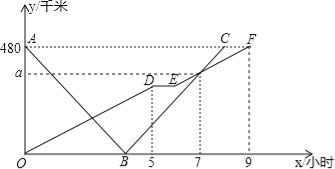
”¾½āĪö”æŹŌĢā·ÖĪö£ŗ£Ø1£©ÓÉĖŁ¶Č=Ā·³Ģ”ĀŹ±¼ä¼“æÉµĆ³öĀż³µµÄĖŁ¶Č£¬aĖł¶ŌÓ¦µÄŹ±¼äĪŖ7£¬ÓÉĀ·³Ģ=ĖŁ¶Č”ĮŹ±¼ä£¬æÉµĆ³öaµÄÖµ£»
£Ø2£©ÉčĻąÓöŹ±¼äĪŖt£¬½įŗĻĶ¼ŠĪĒó³öæģ³µµÄĖŁ¶Č£¬ĄūÓĆĻąÓöŹ±¼ä=Į½µŲ¾ąĄė”ĀĮ½³µĖŁ¶ČÖ®ŗĶ£¬æÉµĆ³öĻąÓöŹ±¼ä£¬ŌŁÓÉĀ·³Ģ=ĖŁ¶Č”ĮŹ±¼ä¼“æÉµĆ³ö½įĀŪ£»
£Ø3£©½įŗĻæģĀż³µĖŁ¶ČÓėĮ½µŲ¾ąĄė£¬ÕŅ³öB”¢C”¢D”¢EµćµÄ×ų±ź£¬ÓÉĻ߶ĪÉĻµÄĮ½µć×ų±źæÉÕŅ³öøöĻ߶ĪµÄ½āĪöŹ½£¬ĄūÓĆĀ·³ĢĻą¼õ=160¼“æÉÕŅ³ö½įĀŪ£®
½ā£ŗ£Ø1£©Āż³µµÄŠŠŹ»ĖŁ¶ČĪŖ480”Ā£Ø9©1£©=60£ØĒ§Ć×/Ź±£©£¬
a=£Ø7©1£©”Į60=360£®
£Ø2£©æģ³µµÄŠŠŹ»ĖŁ¶ČĪŖ£Ø480+360£©”Ā7=120£ØĒ§Ć×/Ź±£©£¬
ÉčĮ½³µĻąÓöŹ±¼äĪŖ480”Ā£Ø60+120£©=![]() £ØŠ”Ź±£©£¬
£ØŠ”Ź±£©£¬
120”Į![]() =320£ØĒ§Ć×£©£®
=320£ØĒ§Ć×£©£®
“š£ŗæģ³µÓėĀż³µµŚŅ»“ĪĻąÓöŹ±£¬¾ąĄė¼×µŲµÄĀ·³ĢŹĒ320Ē§Ć×£®
£Ø3£©480”Ā120=4£ØŠ”Ź±£©£¬
¹ŹBµć×ų±źĪŖ£Ø4£¬0£©£®
4”Į2=8£ØŠ”Ź±£©£¬
¹ŹCµć×ų±źĪŖ£Ø8£¬480£©£®
60”Į5=300£ØĒ§Ć×£©£¬
¹ŹDµć×ų±źĪŖ£Ø5£¬300£©£¬Eµć×ų±źĪŖ£Ø6£¬300£©£®
½įŗĻĶ¼ŠĪæÉÖŖ£ŗAB£ŗy=©120x+180£Ø0”Üx”Ü4£©£»BC£ŗy=120x©480£Ø4”Üx”Ü8£©£»OD£ŗy=60x£Ø0”Üx”Ü5£©£»DE£ŗy=300£Ø5”Üx”Ü6£©£»EF£ŗy=60x©60£Ø7”Üx”Ü9£©£®
ÓÉ©120x+180©60x=160£¬½āµĆx=![]() £»
£»
ÓÉ60x©£Ø©120x+180£©=160£¬½āµĆx=![]() £»
£»
ÓÉ300©£Ø©120x+180£©=160£¬½āµĆx=![]() £»
£»
ÓÉ120x©480©£Ø60x©60£©=160£¬½āµĆx=![]() £ØÉįČ„£©£®
£ØÉįČ„£©£®
¹Ź£ŗĮ½³µ³ö·¢ŗó![]() ”¢
Ӣ![]() Ӣ
”¢![]() Š”Ź±Ļą¾ąµÄĀ·³ĢĪŖ160Ē§Ć×£®
Š”Ź±Ļą¾ąµÄĀ·³ĢĪŖ160Ē§Ć×£®


 µ¼Ń§½Ģ³ĢøßÖŠŠĀæĪ±źĻµĮŠ“š°ø
µ¼Ń§½Ģ³ĢøßÖŠŠĀæĪ±źĻµĮŠ“š°ø Š”ѧæĪŹ±ĢŲѵĻµĮŠ“š°ø
Š”ѧæĪŹ±ĢŲѵĻµĮŠ“š°ø
| Äź¼¶ | øßÖŠæĪ³Ģ | Äź¼¶ | ³õÖŠæĪ³Ģ |
| øßŅ» | øßŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” | ³õŅ» | ³õŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” |
| ø߶ž | ø߶žĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õ¶ž | ³õ¶žĆā·ŃæĪ³ĢĶĘ¼ö£” |
| øßČż | øßČżĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õČż | ³õČżĆā·ŃæĪ³ĢĶĘ¼ö£” |
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æŌŚŅ»“Ī12ČĖ²Ī¼ÓµÄŹżŃ§²āŹŌÖŠ£¬µĆ100·Ö”¢95·Ö”¢90·Ö”¢85·Ö”¢75·ÖµÄČĖŹż·Ö±šĪŖ1”¢3”¢4”¢2”¢2£¬ÄĒĆ“Õā×鏿¾ŻµÄÖŚŹżŹĒ_____.
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æĻČ»Æ¼ņ£¬ŌŁĒóÖµ£ŗx 2 -£Øx+2£©£Ø2-x£©-2£Øx-5£©2 £¬ĘäÖŠx=3£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æŌŚĘ½ĆęÖ±½Ē×ų±źĻµÄŚ£¬µćP£Ø©2£¬3£©¹ŲÓŚŌµćµÄ¶Ō³ĘµćQµÄ×ų±źĪŖ£Ø £©
A.£Ø2£¬©3£©
B.£Ø2£¬3£©
C.£Ø3£¬©2£©
D.£Ø©2£¬©3£©
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČōŅŃÖŖ|a+2|+|b©3|+|c©4|=0£¬ŌņŹ½×Óa+2b+3cµÄÖµĪŖ________£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼£¬ĖıߊĪABCDĪŖĘ½ŠŠĖıߊĪ£¬ŃÓ³¤ADµ½E£¬Ź¹DE=AD£¬Į¬½ÓEB£¬EC£¬DB£¬Ģķ¼ÓŅ»øöĢõ¼ž£¬²»ÄÜŹ¹ĖıߊĪDBCE³ÉĪŖ¾ŲŠĪµÄŹĒ£Ø £© 
A.AB=BE
B.BE”ĶDC
C.”ĻADB=90”ć
D.CE”ĶDE
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼£¬Å×ĪļĻßy=x2+bx+c¾¹ż×ų±źŌµć£¬²¢ÓėxÖį½»ÓŚµćA£Ø2£¬0£©£®

£Ø1£©Ēó“ĖÅ×ĪļĻߵĽāĪöŹ½£»
£Ø2£©Ēó“ĖÅ×ĪļĻ߶„µć×ų±ź¼°¶Ō³ĘÖį£»
£Ø3£©ČōÅ×ĪļĻßÉĻÓŠŅ»µćB£¬ĒŅS”÷OAB=1£¬ĒóµćBµÄ×ų±ź£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æŅŃÖŖ£¬ČēĶ¼£¬Ö±ĻßAB”¢CD”¢EF¶¼¾¹żµćO£¬ĒŅAB”ĶCD£¬OGĘ½·Ö”ĻBOE£¬Čē¹ū”ĻEOG= ![]() ”ĻAOE£¬Ēó”ĻEOGŗĶ”ĻDOFµÄ¶ČŹż£®
”ĻAOE£¬Ēó”ĻEOGŗĶ”ĻDOFµÄ¶ČŹż£® 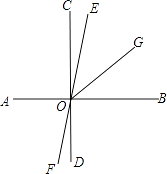
²éæ““š°øŗĶ½āĪö>>
°Ł¶ČÖĀŠÅ - Į·Ļ°²įĮŠ±ķ - ŹŌĢāĮŠ±ķ
ŗž±±Ź”»„ĮŖĶųĪ„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±ØĘ½ĢØ | ĶųÉĻÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | µēŠÅÕ©Ę¾Ł±Ø×ØĒų | É꥜Ź·ŠéĪŽÖ÷ŅåÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | ÉęĘóĒÖČؾŁ±Ø×ØĒų
Ī„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±Øµē»°£ŗ027-86699610 ¾Ł±ØÓŹĻä£ŗ58377363@163.com