
 请从以下两个小题中任选一个作答,若多选,则按第一题计分.
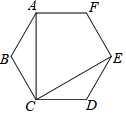
请从以下两个小题中任选一个作答,若多选,则按第一题计分.分析 A.由正六边形性质知∠BAC=∠BCA=30°、∠ACE=60°,作BG⊥AC可得AC=2AG=2ABcos∠BAC=4$\sqrt{3}$,利用扇形面积公式求解可得;
B.利用计算器计算即可得.
解答 解:A.∵正六边形ABCDEF中,AB=BC=CD=DE,∠ABC=∠CDE=∠BCD=120°,
∴∠BAC=∠BCA=∠DCE=∠DEC=30°,
∴∠ACE=60°,
作BG⊥AC于点G,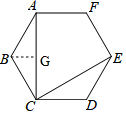
则AC=2AG=2ABcos∠BAC=2×4×$\frac{\sqrt{3}}{2}$=4$\sqrt{3}$,
∴对角线AC扫过的图形面积是$\frac{60•π•(4\sqrt{3})^{2}}{360}$=8π,
故答案为:8π;
B.tan65°+$\sqrt{1.6}$≈2.145+1.265≈3.41,
故答案为:3.41.
点评 本题主要考查正多边形的性质、扇形面积的计算、计算器的使用,熟练掌握正多边形的性质和扇形面积公式是解题的关键.


科目:初中数学 来源: 题型:解答题
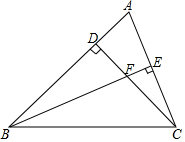 如图,在△ABC中,∠ABC=45°,CD⊥AB于点D,AC的垂直平分线BE与CD交于点F,与AC交于点E.
如图,在△ABC中,∠ABC=45°,CD⊥AB于点D,AC的垂直平分线BE与CD交于点F,与AC交于点E.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
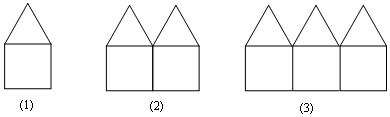
| A. | 66 | B. | 56 | C. | 55 | D. | 61 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
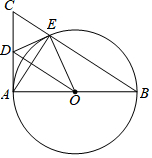 如图,AB是⊙O的直径,AC是⊙O的切线,A为切点,BC交⊙O于点E.
如图,AB是⊙O的直径,AC是⊙O的切线,A为切点,BC交⊙O于点E.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
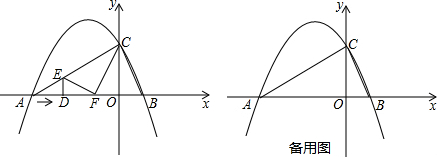
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com