
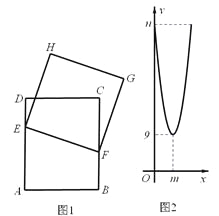
【题目】如图1,A、B、C、D为矩形的四个顶点,AD=4cm,AB=dcm。动点E、F分别从点D、B出发,点E以1 cm/s的速度沿边DA向点A移动,点F以1 cm/s的速度沿边BC向点C移动,点F移动到点C时,两点同时停止移动。以EF为边作正方形EFGH,点F出发xs时,正方形EFGH的面积为ycm2。已知y与x的函数图象是抛物线的一部分,如图2所示。请根据图中信息,解答下列问题:
(1)自变量x的取值范围是 ▲ ;
(2)d= ▲ ,m= ▲ ,n= ▲ ;
(3)F出发多少秒时,正方形EFGH的面积为16cm2?
【答案】(1)0≤x≤4。
(2)3,2,25.
(3)F出发![]() 或
或![]() 秒时,正方形EFGH的面积为16cm2
秒时,正方形EFGH的面积为16cm2
【解析】
(1)自变量x的取值范围是点F从点C到点B的运动时间,由时间=距离÷速度,即可求。
(2)由图2知,正方形EFGH的面积的最小值是9,而正方形EFGH的面积最小时,根据地两平行线间垂直线段最短的性质,得d=AB=EF=3。
当正方形EFGH的面积最小时,由BF=DE和EF∥AB得,E、F分别为AD、BC的中点,即m=2。
当正方形EFGH的面积最大时,EF等于矩形ABCD的对角线,根据勾股定理,它为5,即n=25。
解:(1)0≤x≤4。
(2)3,2,25.
(3)过点E作EI⊥BC垂足为点I。则四边形DEIC为矩形。
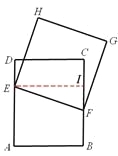
∴EI=DC=3,CI=DE=x。
∵BF=x,∴IF=4-2x。
在Rt△EFI中,![]() 。
。
∵y是以EF为边长的正方形EFGH的面积,
∴![]() 。
。
当y=16时,![]() ,
,
解得,![]() 。
。
∴F出发![]() 或
或![]() 秒时,正方形EFGH的面积为16cm2。
秒时,正方形EFGH的面积为16cm2。
(3)求出正方形EFGH的面积y关于x的函数关系式,即可求得F出发![]() 或
或![]() 秒时,正方形EFGH的面积为16cm2。
秒时,正方形EFGH的面积为16cm2。


 名师点拨卷系列答案
名师点拨卷系列答案 英才计划期末调研系列答案
英才计划期末调研系列答案科目:初中数学 来源: 题型:
【题目】已知关于x的一元二次方程![]() 有实数根.
有实数根.
(1)求m的值;
(2)先作![]() 的图象关于x轴的对称图形,然后将所作图形向左平移3个单位长度,再向上平移2个单位长度,写出变化后图象的解析式.
的图象关于x轴的对称图形,然后将所作图形向左平移3个单位长度,再向上平移2个单位长度,写出变化后图象的解析式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,A(﹣1,2),B(﹣2,﹣1),C(﹣1,﹣1),抛物线y=ax2(a≠0)经过△ABC区域(包括边界),则a的取值范围是_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
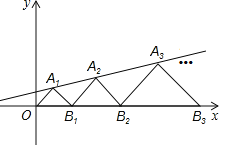
【题目】如图,在平面直角坐标系中,点A1,A2,A3,…和B1,B2,B3,…分别在直线y=![]() x+b和x轴上.△OA1B1,△B1A2B2,△B2A3B3,…都是等腰直角三角形.如果点A1(1,1),那么点A2018的纵坐标是_____.
x+b和x轴上.△OA1B1,△B1A2B2,△B2A3B3,…都是等腰直角三角形.如果点A1(1,1),那么点A2018的纵坐标是_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在菱形ABCD中,对角线AC与BD相交于点O,AB=13,BD=24,在菱形ABCD的外部以AB为边作等边三角形 ABE.点F是对角线BD上一动点(点F不与点B重合),将线段AF绕点A顺时针方向旋转60°得到线段AM,连接FM.
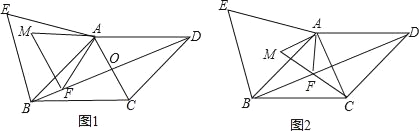
(1)求AO的长;
(2)如图2,当点F在线段BO上,且点M,F,C三点在同一条直线上时,求证:AC=![]() AM;
AM;
(3)连接EM,若△AEM的面积为40,请直接写出△AFM的周长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】郴州市正在创建“全国文明城市”,某校拟举办“创文知识”抢答赛,欲购买A、B两种奖品以鼓励抢答者.如果购买A种20件,B种15件,共需380元;如果购买A种15件,B种10件,共需280元.
(1)A、B两种奖品每件各多少元?
(2)现要购买A、B两种奖品共100件,总费用不超过900元,那么A种奖品最多购买多少件?
查看答案和解析>>
科目:初中数学 来源: 题型:
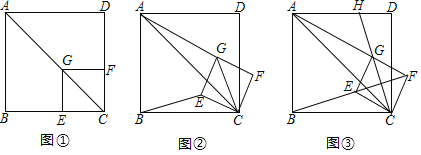
【题目】如图![]() ,已知点G在正方形ABCD的对角线AC上,
,已知点G在正方形ABCD的对角线AC上,![]() ,垂足为点E,
,垂足为点E,![]() ,垂足为点F.
,垂足为点F.
![]() 发现问题:在图
发现问题:在图![]() 中,
中,![]() 的值为______.
的值为______.
![]() 探究问题:将正方形CEGF绕点C顺时针方向旋转
探究问题:将正方形CEGF绕点C顺时针方向旋转![]() 角
角![]() ,如图
,如图![]() 所示,探究线段AG与BE之间的数量关系,并证明你的结论.
所示,探究线段AG与BE之间的数量关系,并证明你的结论.
![]() 解决问题:正方形CEGF在旋转过程中,当B,E,F三点在一条直线上时,如图
解决问题:正方形CEGF在旋转过程中,当B,E,F三点在一条直线上时,如图![]() 所示,延长CG交AD于点H;若
所示,延长CG交AD于点H;若![]() ,
,![]() ,直接写出BC的长度.
,直接写出BC的长度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在矩形ABCD中,∠B的角平分线BE与AD交于点E,∠BED的角平分线EF与DC交于点F,若AB=9,DF=2FC,则BC=____.(结果保留根号)

查看答案和解析>>
科目:初中数学 来源: 题型:
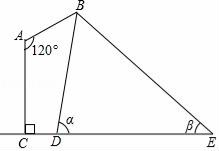
【题目】如图是某路灯在铅垂面内的示意图,灯柱AC的高为11米,灯杆AB与灯柱AC的夹角∠A=120°,路灯采用锥形灯罩,在地面上的照射区域DE长为18米,从D,E两处测得路灯B的仰角分别为α和β,且tanα=6,tanβ=![]() ,求灯杆AB的长度.
,求灯杆AB的长度.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com