
如图,在平面直角坐标系中,点O为坐标原点,正方形OABC的边OA、OC分别在x轴、y轴上,点B的坐标为(2,2),反比例函数 (x>0,k≠0)的图像经过线段BC的中点D.
(x>0,k≠0)的图像经过线段BC的中点D.
⑴求k的值;
⑵若点P(x,y)在该反比例函数的图像上运动(不与点D重合),过点P作PR⊥y轴于点R,作PQ⊥BC所在直线于点Q,记四边形CQPR的面积为S,求S关于x的解析式并写出x的取值范围.
(1)k=2;
(2)S=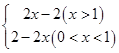 .
.
解析试题分析:(1)首先根据题意求出C点的坐标,然后根据中点坐标公式求出D点坐标,由反比例函数y= (x>0,k≠0)的图象经过线段BC的中点D,D点坐标代入解析式求出k即可;
(x>0,k≠0)的图象经过线段BC的中点D,D点坐标代入解析式求出k即可;
(2)分两步进行解答,①当P在直线BC的上方时,即0<x<1,如图1,根据S四边形CQPR=CQ•PD列出S关于x的解析式,②当P在直线BC的下方时,即x>1,如图2,依然根据S四边形CQPR=CQ•PG列出S关于x的解析式.
试题解析:(1)∵正方形OABC的边OA、OC分别在x轴、y轴上,点B的坐标为(2,2),
∴C(0,2),
∵D是BC的中点,
∴D(1,2),
∵反比例函数y= (x>0,k≠0)的图象经过点D,
(x>0,k≠0)的图象经过点D,
∴k=2;
(2)当P在直线BC的上方时,即0<x<1,
如图1,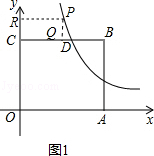
∵点P(x,y)在该反比例函数的图象上运动,
∴y=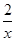 ,
,
∴S四边形CQPR=CQ•PQ=x•(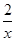 ﹣2)=2﹣2x(0<x<1),
﹣2)=2﹣2x(0<x<1),
当P在直线BC的下方时,即x>1如图2,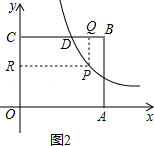
同理求出S四边形CQPR=CQ•CR=x•(2﹣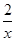 )=2x﹣2(x>1),
)=2x﹣2(x>1),
综上S=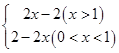 .
.
考点:反比例函数综合题.


科目:初中数学 来源: 题型:解答题
如图,在平面直角坐标系中,直线l与x轴相交于点M,与y轴相交于点N,Rt△MON的外心为点A( ,﹣2),反比例函数y=
,﹣2),反比例函数y= (x>0)的图象过点A.
(x>0)的图象过点A.
(1)求直线l的解析式;
(2)在函数y= (x>0)的图象上取异于点A的一点B,作BC⊥x轴于点C,连接OB交直线l于点P.若△ONP的面积是△OBC面积的3倍,求点P的坐标.
(x>0)的图象上取异于点A的一点B,作BC⊥x轴于点C,连接OB交直线l于点P.若△ONP的面积是△OBC面积的3倍,求点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
已知y=y1-y2,其中y1是x的反比例函数,y2是x2的正比例函数,且x=1时y=3,x=-2时y=-15.
求:(1)y与x之间的函数关系式;
(2)当x=2时y的值.
查看答案和解析>>
科目:初中数学 来源: 题型:计算题
如图,已知A(-4,2)、B(n,-4)是一次函数y=kx+b的图象与反比例函数y=的图象的两个交点.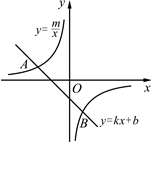
【小题1】求此反比例函数和一次函数的解析式
【小题2】根据图象写出使一次函数的值小于反比例函数的值的x的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com