
【题目】如图,正方形ABCD中,AB=4,点E是边BC的中点,点G,H分别是边CD,AB上的动点,连接GH交AE于F,且使GH⊥AE,连接AG,EH,则EH+AG的最小值是( )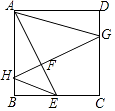
A.8
B.4 ![]()
C.2 ![]()
D.8 ![]()
【答案】C
【解析】如图,由题意易证AE=GH=2 ![]() ,设FH=x,EF=y,则有HE+AG=
,设FH=x,EF=y,则有HE+AG= ![]() +
+ ![]() ,
,
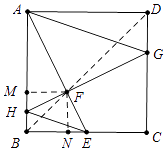
欲求HE+AG的最小值,相当于在平面直角坐标系内找一点(x,y),使得这个点到O(0,0),P(2 ![]() ,2
,2 ![]() )的距离和最小,显然这个点在线段OP上,满足x=y时,HE+AG的值最小,由此可知FH=EF时,HE+AG的值最小,如图连接BD交AE于F,作FM⊥AB于M,FN⊥BC于N,易证△FMH≌△FNE,
)的距离和最小,显然这个点在线段OP上,满足x=y时,HE+AG的值最小,由此可知FH=EF时,HE+AG的值最小,如图连接BD交AE于F,作FM⊥AB于M,FN⊥BC于N,易证△FMH≌△FNE,
∴FH=EF,此时HE+AG的值最小,
易证四边形BNFM是正方形,设边长为a,则有 ![]() =
= ![]() ,
,
∴ ![]() =
= ![]() ,
,
∴a= ![]() ,
,
∴EF=FH= ![]() =
= ![]() ,
,
∴x=y= ![]() ,
,
∴HE+AG的最小值=2 ![]() ,
,
所以答案是:C.
解法二:作GK⊥AB于K,作EM∥AG,GM∥AE,则四边形AEGM是平行四边形.
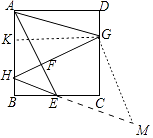
∵AE⊥HG,
∴∠B=∠GKH=∠AFH=90°,
∴∠BAE+∠AHF=90°,∠AHF+∠KGH=90°,
∴∠BAE=∠KGH,
∵KG=BC=AB,
∴△KGH≌△BAE,
∴GH=AG,
∴AE=GM=HG,AG=EM,
∴△GHM是等腰直角三角形,GH=GM=AE=2 ![]() ,
,
∵AG+HE=EM+EG,
∴当H、E、M共线时,AG+HE的值最小,最小值= ![]() HG=2
HG=2 ![]() .
.
所以答案是:C.
【考点精析】通过灵活运用正方形的性质和轴对称-最短路线问题,掌握正方形四个角都是直角,四条边都相等;正方形的两条对角线相等,并且互相垂直平分,每条对角线平分一组对角;正方形的一条对角线把正方形分成两个全等的等腰直角三角形;正方形的对角线与边的夹角是45o;正方形的两条对角线把这个正方形分成四个全等的等腰直角三角形;已知起点结点,求最短路径;与确定起点相反,已知终点结点,求最短路径;已知起点和终点,求两结点之间的最短路径;求图中所有最短路径即可以解答此题.


科目:初中数学 来源: 题型:
【题目】如图,△ABC的顶点都在网格点上,建立如图所示的平面直角坐标系.
(1)请根据如图所示的平面直角坐标系,写出△ABC各点的坐标,并求出△ABC的面积.
(2)把△ABC平移到△A1B1C1,使点B1与原点O重合,按要求画出△A1B1C1,并写出平移过程.
(3)已知P是△ABC内有一点,平移至△A1B1C1后,P点对应点的坐标为P1 (a,b),试写出P点的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,排球运动员站在点O处练习发球,将球从O点正上方2m的A处发出,把球看成点,其运行的高度y(m)与运行的水平距离x(m)满足关系式y=a(x﹣6)2+h.已知球网与O点的水平距离为9m,高度为2.43m,球场的边界距O点的水平距离为18m.
(1)当h=2.6时,求y与x的关系式(不要求写出自变量x的取值范围)
(2)当h=2.6时,球能否越过球网?球会不会出界?请说明理由;
(3)若球一定能越过球网,又不出边界,求h的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数y=kx+b与反比例函数y= ![]() (x>0)的图象交于A(m,6),B(3,n)两点,与x轴交于点C,与y轴交于点D,下列结论:①一次函数解析式为y=﹣2x+8;②AD=BC;③kx+b﹣
(x>0)的图象交于A(m,6),B(3,n)两点,与x轴交于点C,与y轴交于点D,下列结论:①一次函数解析式为y=﹣2x+8;②AD=BC;③kx+b﹣ ![]() <0的解集为0<x<1或x>3;④△AOB的面积是8,其中正确结论的个数是( )
<0的解集为0<x<1或x>3;④△AOB的面积是8,其中正确结论的个数是( )
A.4个
B.3个
C.2个
D.1个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某电信公司提供了A,B两种方案的移动通讯费用y(元)与通话时间x(元)之间的关系,下列结论:
①若通话时间少于120分,则A方案比B方案便宜20元;
②若通话时间超过200分,则B方案比A方案便宜12元;
③若通讯费用为60元,则B方案比A方案的通话时间多;
④若两种方案通讯费用相差10元,则通话时间是145分或185分.其中正确结论的序号是 . 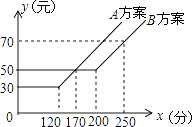
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列命题中,真命题有( )
①直线外一点与直线上各点连接的所有线段中,垂线段最短;
②三角形的一个外角大于任何一个内角;
③如果∠1和∠2是对顶角,那么![]() ;
;
④如果一条直线和两条直线中的一条垂直,那么这条直线也和另一条垂直.
A.1个B.2个C.3个D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】大于1的正整数m的三次幂可“分裂”成若干个连续奇数的和,如23=3+5,33=7+9+11,43=13+15+17+19,…若m3分裂后,其中有一个奇数是2015,则m的值是( )
A.43B.44C.45D.46
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小宇家附近新修了一段公路,他想给市政写信,建议在路的两边种上银杏树![]() 他先让爸爸开车驶过这段公路,发现速度为60千米
他先让爸爸开车驶过这段公路,发现速度为60千米![]() 小时,走了约3分钟,由此估算这段路长约______千米.
小时,走了约3分钟,由此估算这段路长约______千米.
然后小宇查阅资料,得知银杏为落叶大乔木,成年银杏树树冠直径可达8米![]() 小宇计划从路的起点开始,每隔a米种一棵树,绘制示意图如图:
小宇计划从路的起点开始,每隔a米种一棵树,绘制示意图如图:
考虑到投入资金的限制,他设计了另一种方案,将原计划的a扩大一倍,则路的两侧共计减少200棵数,请你求出a的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com