
科目:初中数学 来源: 题型:选择题
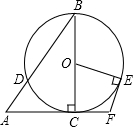 如图,在Rt△ABC中,∠ACB=90°,∠A=56°.以BC为直径的⊙O交AB于点D.E是⊙O上一点,且$\widehat{C{E}}$=$\widehat{CD}$,连接OE.过点E作EF⊥OE,交AC的延长线于点F,则∠F的度数为( )
如图,在Rt△ABC中,∠ACB=90°,∠A=56°.以BC为直径的⊙O交AB于点D.E是⊙O上一点,且$\widehat{C{E}}$=$\widehat{CD}$,连接OE.过点E作EF⊥OE,交AC的延长线于点F,则∠F的度数为( )| A. | 92° | B. | 108° | C. | 112° | D. | 124° |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
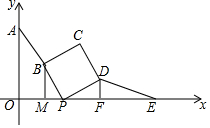 如图,已知A(0,4),E(8,0),点P(a,0)是线段OE上的动点,点B为AP的中点,以BP为边向右边作正方形PBCD,过点B作BM⊥x轴于点M,过点D作DF⊥x轴于点F,连接DE.
如图,已知A(0,4),E(8,0),点P(a,0)是线段OE上的动点,点B为AP的中点,以BP为边向右边作正方形PBCD,过点B作BM⊥x轴于点M,过点D作DF⊥x轴于点F,连接DE.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| 30 | $\sqrt{4}$ | 2$\sqrt{3}$sin60° | 22 |
| -3 | -2 | -$\sqrt{2}$sin45° | 0 |
| |-5| | 6 | 23 | |
| ($\frac{1}{3}$)-1 | 4 | $\sqrt{25}$ | ($\frac{1}{6}$)-1 |
| A. | 5 | B. | 6 | C. | 7 | D. | 8 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 2016年11月1日,万众期待的歼20战机现身珠海航展,上午9时,某航空爱好者在地面C处测得点A处的歼20战机的仰角是30°,正以300米/秒的速度向正西方向航行,1分钟后到达点B处,此时航空爱好者测得其仰角为45°,如图所示,求歼20战机在珠海航展表演时的飞行高度.(精确到100米)参考数据:$\sqrt{2}$≈1.41,$\sqrt{3}$≈1.73.
2016年11月1日,万众期待的歼20战机现身珠海航展,上午9时,某航空爱好者在地面C处测得点A处的歼20战机的仰角是30°,正以300米/秒的速度向正西方向航行,1分钟后到达点B处,此时航空爱好者测得其仰角为45°,如图所示,求歼20战机在珠海航展表演时的飞行高度.(精确到100米)参考数据:$\sqrt{2}$≈1.41,$\sqrt{3}$≈1.73.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
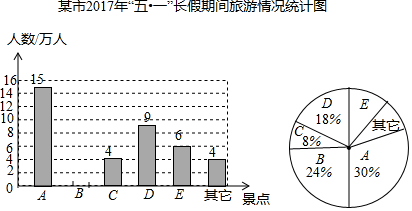
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com