
分析 (1)设A商品的进价为x元/件,则B商品的进价为3x元/件,根据3件A商品和1件B商品恰好用360元,即可得出关于x的一元一次方程,解之即可得出结论;
(2)设购进A商品m件,则购进B商品(100-m)件,根据总价=单价×购进数量结合总费用不少于14100元且不超过14500元,即可得出关于m的一元一次不等式组,解之即可得出m的取值范围,取其内的整数即可得出进货方案数,设商品全部销售完商店的利润为w,根据总利润=单价利润×购进数量,即可得出w关于m的函数关系式,利用一次函数的性质即可解决最值问题.
解答 解:(1)设A商品的进价为x元/件,则B商品的进价为3x元/件,
根据题意得:3x+3x=360,
解得:x=60,
∴3x=180.
答:A商品的进价为60元/件,B商品的进价为180元/件.
(2)设购进A商品m件,则购进B商品(100-m)件,
根据题意得:$\left\{\begin{array}{l}{60m+180(100-m)≥14100}\\{60m+180(100-m)≤14500}\end{array}\right.$,
解得:29$\frac{1}{6}$≤m≤32$\frac{1}{2}$.
∵m为整数,
∴30≤m≤32,
∴m=30、31或32.
∴该商店有三种进货方案.
设商品全部销售完商店的利润为w,
根据题意得:w=(100-60)m+(230-180)(100-m)=-10m+5000,
∵-10<0,
∴当m=30时,w取最大值,最大值为4700.
故当购进A商品30件、B商品70件时,该商店可获得最大利润,最大利润为4700元.
点评 本题考查了一元一次方程的应用、一元一次不等式组的应用以及一次函数的最值,解题的关键是:(1)根据3件A商品和1件B商品恰好用360元,列出关于x的一元一次方程;(2)根据总价=单价×购进数量结合总价的范围,列出关于m的一元一次不等式组.


 英语小英雄天天默写系列答案
英语小英雄天天默写系列答案 暑假作业安徽少年儿童出版社系列答案
暑假作业安徽少年儿童出版社系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,AB是⊙O的切线,B为切点,若∠ABC=120°,AB=2$\sqrt{3}$,AC经过点O,与⊙O分别相交于点D,C,则阴影部分的面积是( )
如图,AB是⊙O的切线,B为切点,若∠ABC=120°,AB=2$\sqrt{3}$,AC经过点O,与⊙O分别相交于点D,C,则阴影部分的面积是( )| A. | 2$\sqrt{3}$ | B. | $\frac{π}{6}$ | C. | 4$\sqrt{3}$-$\frac{2π}{3}$ | D. | 2$\sqrt{3}$-$\frac{2π}{3}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
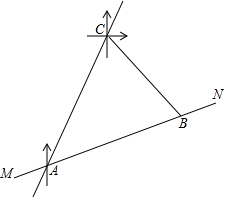 超速行驶是一种十分危险的违法驾驶行为,在一条笔直的高速公路MN上,小型车限速为每小时120千米,设置在公路旁的超速监测点C,现测得一辆小型车在监测点C的南偏西30°方向的A处,7秒后,测得其在监测点C的南偏东45°方向的B处,已知BC=200米,B在A的北偏东75°方向,请问:这辆车超速了吗?通过计算说明理由.(参考数据:$\sqrt{2}$≈1.41,$\sqrt{3}$≈1.73)
超速行驶是一种十分危险的违法驾驶行为,在一条笔直的高速公路MN上,小型车限速为每小时120千米,设置在公路旁的超速监测点C,现测得一辆小型车在监测点C的南偏西30°方向的A处,7秒后,测得其在监测点C的南偏东45°方向的B处,已知BC=200米,B在A的北偏东75°方向,请问:这辆车超速了吗?通过计算说明理由.(参考数据:$\sqrt{2}$≈1.41,$\sqrt{3}$≈1.73)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com