
【题目】如图,在Rt△ABC中,∠ABC=90°,CD⊥BC,BD与AC相交于点E,AB=9,BC=4,DC=3.
(1)求BE的长度;
(2)求△ABE的面积.

【答案】(1)![]() ;(2)
;(2)![]() .
.
【解析】试题分析:
(1)先在Rt△BCD中,由勾股定理求得BD的长;再证△ABE∽△CDE,利用相似三角形对应边成比例即可解得BE的长;
(2)如图,作EF⊥AB于点F,延长FE交CD于点H,由已知可证得FH=BC=4,FH⊥CD,由(1)中所得△ABE∽△CDE结合“相似三角形对应边上的高之比等于相似比”可得EF:EH=DC:AB=1:3,从而可解得EF的长,即可求得△ABE的面积.
试题解析:
解:(1)∵CD⊥BC,
∴∠DCB=90°,
在Rt△BCD中,BC=4,DC=3,
根据勾股定理得:BD=![]() =5,
=5,
∵AB∥CD,
∴△ABE∽△CDE,
∴DC:AB=DE:BE=3:9=1:3,
又∵BD=5,
∴BE=![]() BD=
BD=![]() ;
;
(2)作EF⊥AB,交CD与点H,可得EH⊥CD,
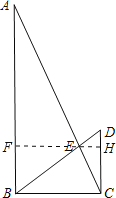
∵△ABE∽△CDE,
∴EF:EH=DC:AB=1:3,
又∵BC=4,
∴FE=![]() BC=3,
BC=3,
则S△ABE=AB×EF×![]() =
=![]() .
.


科目:初中数学 来源: 题型:
【题目】如图,在边长为1的正方形组成的网格中建立直角坐标系,△AOB的顶点均在格点上,点O为原点,点A、B的坐标分别是A(3,2)、B(1,3).

(1)将△AOB向下平移3个单位后得到△A1O1B1,则点B1的坐标为 ;
(2)将△AOB绕点O逆时针旋转90°后得到△A2OB2,请在图中作出△A2OB2,并求出这时点A2的坐标为 ;
(3)在(2)中的旋转过程中,线段OA扫过的图形的面积 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了抓住梵净山文化艺术节的商机,某商店决定购进A、B两种艺术节纪念品.若购进A种纪念品8件,B种纪念品3件,需要950元;若购进A种纪念品5件,B种纪念品6件,需要800元.
(1)求购进A、B两种纪念品每件各需多少元?
(2)若该商店决定购进这两种纪念品共100件,考虑市场需求和资金周转,用于购买这100件纪念品的资金不少于7500元,但不超过7650元,那么该商店共有几种进货方案?
(3)若销售每件A种纪念品可获利润20元,每件B种纪念品可获利润30元,在第(2)问的各种进货方案中,哪一种方案获利最大?最大利润是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在![]() 中,
中,![]() 边的垂直平分线
边的垂直平分线![]() 交
交![]() 于点
于点![]() ,
,![]() 边的垂直平分线
边的垂直平分线![]() 交
交![]() 于点
于点![]() ,
,![]() 与
与![]() 相交于点
相交于点![]() ,联结
,联结![]() 、
、![]() ,若
,若![]() 的周长为
的周长为![]() ,
,![]() 的周长为
的周长为![]() .
.

(1)求线段![]() 的长;
的长;
(2)联结![]() ,求线段
,求线段![]() 的长;
的长;
(3)若![]() ,求
,求![]() 的度数.
的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,△ABC的三个顶点分别是A(-2,0),B(0,3),C(3,0).
(1)在所给的图中,画出这个平面直角坐标系;
(2)点A经过平移后对应点为D(3,-3),将△ABC作同样的平移得到△DEF,点B的对应点为点E,画出平移后的△DEF;
(3)在(2)的条件下,点M在直线CD上,若DM=2CM,直接写出点M的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,如图,在四边形ABCD中,AB∥CD,E,F为对角线AC上两点,且AE=CF,DF∥BE,AC平分∠BAD.求证:四边形ABCD为菱形.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一次课题学习活动中,老师提出了如下问题:如图,四边形![]() 是正方形,点
是正方形,点![]() 是边
是边![]() 的中点,
的中点,![]() ,且
,且![]() 交正方形外角平分线
交正方形外角平分线![]() 于点
于点![]() .请你探究
.请你探究![]() 与
与![]() 存在怎样的数量关系,并证明你的结论正确.经过探究,小明得出的结论是
存在怎样的数量关系,并证明你的结论正确.经过探究,小明得出的结论是![]() ,而要证明结论
,而要证明结论![]() ,就需要证明
,就需要证明![]() 和
和![]() 所在的两个三角形全等,但
所在的两个三角形全等,但![]() 和
和![]() 显然不全等(一个是直角三角形,一个是钝角三角形),考虑到点
显然不全等(一个是直角三角形,一个是钝角三角形),考虑到点![]() 是边
是边![]() 的中点,小明想到的方法是如图2,取
的中点,小明想到的方法是如图2,取![]() 的中点
的中点![]() ,连接
,连接![]() ,证明
,证明![]() .从而得到
.从而得到![]() .请你参考小明的方法解决下列问题.
.请你参考小明的方法解决下列问题.
(1)如图3,若把条件“点![]() 是边
是边![]() 的中点”改为“点
的中点”改为“点![]() 是边
是边![]() 上的任意一点”,其余条件不变,证明结论
上的任意一点”,其余条件不变,证明结论![]() 仍然成立;
仍然成立;
(2)如图4,若把条件“点![]() 是边
是边![]() 的中点”改为:“点
的中点”改为:“点![]() 是边
是边![]() 延长线上的一点”,其余条件仍不变,那么结论
延长线上的一点”,其余条件仍不变,那么结论![]() 是否还成立?若成立,请完成证明过程,若不成立,请说明理由.
是否还成立?若成立,请完成证明过程,若不成立,请说明理由.




查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在“爱满扬州”慈善一日捐活动中,学校团总支为了了解本校学生的捐款情况,随机抽取了50名学生的捐款数进行了统计,并绘制成统计图.

(1)这50名同学捐款的众数为 元,中位数为 元;
(2)求这50名同学捐款的平均数;
(3)该校共有600名学生参与捐款,请估计该校学生的捐款总数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com