
【题目】菱形![]() 的顶点C与原点O重合,点B落在y轴正半轴上,点A、D落在第一象限内,且D点坐标为
的顶点C与原点O重合,点B落在y轴正半轴上,点A、D落在第一象限内,且D点坐标为![]() .
.
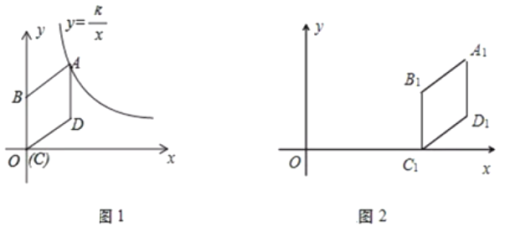
(1)如图1,若反比例函数![]() (
(![]() )的图象经过点A,求k的值;
)的图象经过点A,求k的值;
(2)菱形![]() 向右平移t个单位得到菱形
向右平移t个单位得到菱形![]() ,如图2.
,如图2.
①请直接写出点![]() 、
、![]() 的坐标(用合1的代数式表示):
的坐标(用合1的代数式表示):![]() 、
、![]() ;
;
②是否存在反比例函数![]() (
(![]() ),使得点
),使得点![]() 、
、![]() 同时落在
同时落在![]() (
(![]() )的图象上?若存在,求n的值;若不存在,请说明理由.
)的图象上?若存在,求n的值;若不存在,请说明理由.
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】某校开展了“互助、平等、感恩、和谐、进取”主题班会活动,活动后,就活动的![]() 个主题进行了抽样调查(每位同学只选最关注的一个),根据调查结果绘制了两幅不完整的统计图.根据图中提供的信息,解答下列问题:
个主题进行了抽样调查(每位同学只选最关注的一个),根据调查结果绘制了两幅不完整的统计图.根据图中提供的信息,解答下列问题:
(1)这次调查的学生共有多少名?
(2)请将条形统计图补充完整,并在扇形统计图中计算出“进取”所对应的圆心角的度数.
(3)如果要在这![]() 个主题中任选两个进行调查,根据(2)中调查结果,用树状图或列表法,求恰好选到学生关注最多的两个主题的概率(将互助、平等、感恩、和谐、进取依次记为A、B、C、D、E).
个主题中任选两个进行调查,根据(2)中调查结果,用树状图或列表法,求恰好选到学生关注最多的两个主题的概率(将互助、平等、感恩、和谐、进取依次记为A、B、C、D、E).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,![]() 和
和![]() 是有公共顶点的直角三角形,
是有公共顶点的直角三角形,![]() ,点
,点![]() 为射线
为射线![]() ,
,![]() 的交点.
的交点.
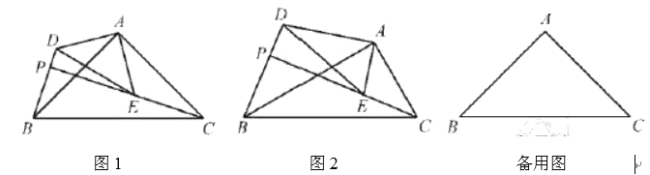
(1)如图1,若![]() 和
和![]() 是等腰三角形,求证:
是等腰三角形,求证:![]() ;
;
(2)如图2,若![]() ,问:(1)中的结论是否成立?请说明理.
,问:(1)中的结论是否成立?请说明理.
(3)在(1)的条件下,![]() ,
,![]() ,若把
,若把![]() 绕点
绕点![]() 旋转,当
旋转,当![]() 时,请直接写出
时,请直接写出![]() 的长度.
的长度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(问题实验)如图①,在地面![]() 上有两根等长立柱
上有两根等长立柱![]() ,
,![]() 之间悬挂一根近似成抛物线
之间悬挂一根近似成抛物线![]() 的绳子.
的绳子.
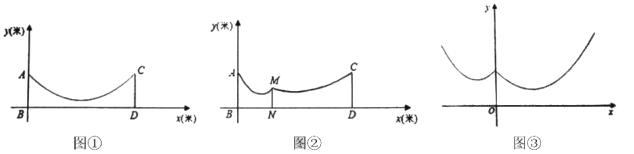
(1)求绳子最低点到地面的距离;
(2)如图②,因实际需要,需用一根立柱![]() 撑起绳子.
撑起绳子.
①若在离![]() 为4米的位置处用立柱
为4米的位置处用立柱![]() 撑起,使立柱左侧的抛物线的最低点距
撑起,使立柱左侧的抛物线的最低点距![]() 为1米,离地面1.8米,求
为1米,离地面1.8米,求![]() 的长;
的长;
②将立柱![]() 来回移动,移动过程中,在一定范围内,总保持立柱
来回移动,移动过程中,在一定范围内,总保持立柱![]() 左侧抛物线的形状不变,其函数表达式为
左侧抛物线的形状不变,其函数表达式为![]() ,当抛物线最低点到地面距离为0.5米时,求
,当抛物线最低点到地面距离为0.5米时,求![]() 的值.
的值.
(问题抽象)如图③,在平面直角坐标系中,函数![]() 的图像记为
的图像记为![]() ,函数
,函数![]() 的图像记为
的图像记为![]() ,其中
,其中![]() 是常数,图像
是常数,图像![]() 、
、![]() 合起来得到的图像记为
合起来得到的图像记为![]() .
.
设![]() 在
在![]() 上的最低点纵坐标为
上的最低点纵坐标为![]() ,当
,当![]() 时,直接写出
时,直接写出![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线![]()
![]() 的图象与x轴交于A,B两点,与y轴交于点C,且关于直线
的图象与x轴交于A,B两点,与y轴交于点C,且关于直线![]() 对称,点A的坐标为(﹣1,0).
对称,点A的坐标为(﹣1,0).
(Ⅰ)求抛物线C的解析式和顶点坐标;
(Ⅱ)将抛物线![]() 绕点O顺时针旋转180°得抛物线
绕点O顺时针旋转180°得抛物线![]() ,且有点P(m,t)既在抛物线
,且有点P(m,t)既在抛物线![]() 上,也在抛物线
上,也在抛物线![]() 上,求m的值;
上,求m的值;
(Ⅲ)当![]() 时,二次函数
时,二次函数![]() 的最小值为
的最小值为![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】课外兴趣小组为了解某段路上机动车的车速,抽查了一段时间内若干辆车的车速(车速取整数,单位:千米/时)并制成如图所示的频数分布直方图.已知车速在41千米/时到50千米/时的车辆数占车辆总数的![]() .
.

(1)在这段时间内他们抽查的车有 辆;
(2)被抽查车辆的车速的中位数所在速度段(单位:千米/时)是( )
A.30.5~40.5 B.40.5~50.5 C.50.5~60.5 D.60.5~70.5
(3)补全频数分布直方图;
(4)如果全天超速(车速大于60千米/时)的车有200辆,则当天的车流量约为多少辆?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两台机床同时加工一批直径为100毫米的零件,为了检验产品的质量,从产品中随机抽查6件进行测量,测得的数据如下:(单位:毫米)甲机床:99 98 100 100 103乙机床:99 100 102 99 100 100则加工这批零件性能较好的机床是_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小楠是一个乐学习,善思考,爱探究的同学,她对函数![]() 的图象和性质进行了探究,请你将下列探究过程补充完整:
的图象和性质进行了探究,请你将下列探究过程补充完整:
(1)函数![]() 的自变量
的自变量![]() 的取值范围是________________;
的取值范围是________________;
(2)用描点法画函数图象:
①列表:
| … | -5 | -2 | -1 | 0 | … | 2 | 3 | 4 | 7 | … |
| … |
| 2 | 3 |
| … | 6 | 3 | 2 | 1 | … |
表中![]() 的值为______________,
的值为______________,![]() 的值为_______________.
的值为_______________.
②描点连线:请在右图画出该图象的另一部分.
(3)观察函数图象,得到函数![]() 的性质之一:当
的性质之一:当![]() _____________时,函数值
_____________时,函数值![]() 随
随![]() 的增大而增大.
的增大而增大.
(4)应用:若![]() ,则
,则![]() 的取值范围是______________.
的取值范围是______________.
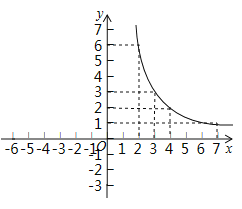
查看答案和解析>>
科目:初中数学 来源: 题型:
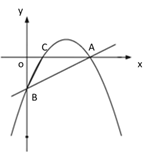
【题目】【题目】如图①,一次函数 y=![]() x - 2 的图像交 x 轴于点 A,交 y 轴于点 B,二次函数 y=
x - 2 的图像交 x 轴于点 A,交 y 轴于点 B,二次函数 y=![]() x2 bx c的图像经过 A、B 两点,与 x 轴交于另一点 C.
x2 bx c的图像经过 A、B 两点,与 x 轴交于另一点 C.
(1)求二次函数的关系式及点 C 的坐标;
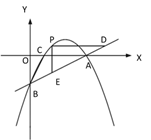
(2)如图②,若点 P 是直线 AB 上方的抛物线上一点,过点 P 作 PD∥x 轴交 AB 于点 D,PE∥y 轴交 AB 于点 E,求 PD+PE 的最大值;
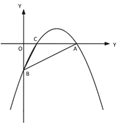
(3)如图③,若点 M 在抛物线的对称轴上,且∠AMB=∠ACB,求出所有满足条件的点 M的坐标.
① ② ③
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com