
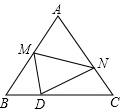
 如图,等边△ABC的边长为10,点M是边AB上一动点,将等边△ABC沿过点M的直线折叠,该直线与直线AC交于点N,使点A落在直线BC上的点D处,且BD:DC=1:4,折痕为MN,则AN的长为7或$\frac{65}{3}$.
如图,等边△ABC的边长为10,点M是边AB上一动点,将等边△ABC沿过点M的直线折叠,该直线与直线AC交于点N,使点A落在直线BC上的点D处,且BD:DC=1:4,折痕为MN,则AN的长为7或$\frac{65}{3}$. 分析 此题要分两种情况进行讨论:①当点A落在线段BC上时;②当A在CB的延长线上时,首先证明△BMD∽△CDN.根据相似三角形的性质可得$\frac{BD}{CN}$=$\frac{DM}{DN}$=$\frac{BM}{CD}$,再设AN=x,则CN=30-x,然后利用含x的式子表示DM、BM,根据BM+DM=30列出方程,解出x的值可得答案.
解答 解:①当点A落在如图1所示的位置时,
∵△ACB是等边三角形,
∴∠A=∠B=∠C=∠MDN=60°,
∵∠MDC=∠B+∠BMD,∠B=∠MDN,
∴∠BMD=∠NDC,
∴△BMD∽△CDN.
∴得$\frac{BD}{CN}$=$\frac{DM}{DN}$=$\frac{BM}{CD}$,
∵DN=AN,
∴得$\frac{BD}{CN}$=$\frac{DN}{AN}$=$\frac{BM}{CD}$,
∵BD:DC=1:4,BC=10,
∴DB=2,CD=8,
设AN=x,则CN=10-x,
∴$\frac{2}{10-x}$=$\frac{DM}{x}$=$\frac{BM}{8}$,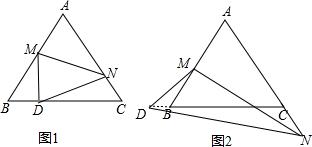
∴DM=$\frac{2x}{10-x}$,BM=$\frac{16}{10-x}$,
∵BM+DM=30,
∴$\frac{2x}{10-x}$+$\frac{16}{10-x}$=10,
解得x=7,
∴AN=7;
②当A在CB的延长线上时,如图2,
与①同理可得△BMD∽△CDN.
∴得$\frac{BD}{CN}$=$\frac{DM}{DN}$=$\frac{BM}{CD}$,
∵BD:DC=1:4,BC=10,
∴DB=$\frac{10}{3}$,CD=$\frac{40}{3}$,
设AN=x,则CN=x-10,
∴$\frac{\frac{10}{3}}{x-10}$=$\frac{DM}{x}$=$\frac{BM}{\frac{40}{3}}$,
∴DM=$\frac{10x}{3(x-10)}$,BM=$\frac{400}{9(x-10)}$,
∵BM+DM=10,
∴$\frac{10x}{3(x-10)}$+$\frac{400}{9(x-10)}$=10,
解得:x=$\frac{65}{3}$,
∴AN=$\frac{65}{3}$.
故答案为:7或$\frac{65}{3}$.
点评 此题主要考查了相似综合题、翻折变换,关键是证明△BMD∽△CDN得到得$\frac{BD}{CN}$=$\frac{DM}{DN}$=$\frac{BM}{CD}$,再利用含AN的式子表示DM、BM.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,在矩形ABCD中,AB<AD,E为AD边上一点,且AE=$\frac{1}{2}$AB,连结BE,将△ABE沿BE翻折,若点A恰好落在CE上点F处,则∠CBF的余弦值为( )
如图,在矩形ABCD中,AB<AD,E为AD边上一点,且AE=$\frac{1}{2}$AB,连结BE,将△ABE沿BE翻折,若点A恰好落在CE上点F处,则∠CBF的余弦值为( )| A. | $\frac{2}{3}$ | B. | $\frac{4}{5}$ | C. | $\frac{\sqrt{3}}{2}$ | D. | $\frac{3}{5}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在平面直角坐标系中,已知△ABC三个顶点的坐标分别为A(-1,2),B(-3,4),C(-2,6).
如图,在平面直角坐标系中,已知△ABC三个顶点的坐标分别为A(-1,2),B(-3,4),C(-2,6).查看答案和解析>>
科目:初中数学 来源: 题型:填空题
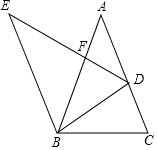 如图△EDB由△ABC绕点B逆时针旋转而来,D点落在AC上,DE交AB于点F,若AB=AC,DB=BF,则AF与BF的比值为$\frac{\sqrt{5}-1}{2}$.
如图△EDB由△ABC绕点B逆时针旋转而来,D点落在AC上,DE交AB于点F,若AB=AC,DB=BF,则AF与BF的比值为$\frac{\sqrt{5}-1}{2}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 某飞机模型的机翼形状如图所示,其中AB∥DC,∠BAE=90°,根据图中的数据求CD的长?(精确到1cm)(参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75)
某飞机模型的机翼形状如图所示,其中AB∥DC,∠BAE=90°,根据图中的数据求CD的长?(精确到1cm)(参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75)查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com