
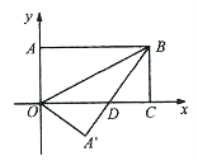
【题目】如图,把长方形纸片OABC放入平面直角坐标系中,使OC、OA分别与x轴,y轴重合,连接OB,将长方形纸片OABC沿OB折叠,使点A落在点A,的位置,A,B与x轴交于D,若点B的坐标为(4,2),则点A,的坐标为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
【答案】D
【解析】
根据折叠性质,设OD=x,在Rt△BDC中勾股定理,得A,D=1.5,OA,=AO=2, 由△OA,D面积可得:A,E![]() DO=OA,
DO=OA,![]() A,D,求出A,E和OE的长度即可表示出坐标.
A,D,求出A,E和OE的长度即可表示出坐标.
解:过点A,向坐标轴做垂线,交点为E,F如下图,
由题可知:∠ABO=∠OBA,
∵AB∥CO,
∴∠ABO=∠BOC,
∴∠DOB=∠OBA,,
∴DO=BD,
∵B(4,2),
∴CO=4,BC=2,
设OD=x,则BD=x,DC=4-x,
在Rt△BDC中,BD2=CD2+BC2,即x2=(4-x)2+22,
解得:x=2.5,
∴A,D=4-2.5=1.5,OA,=AO=2,
由△OA,D面积可得:A,E![]() DO=OA,
DO=OA,![]() A,D,
A,D,
∴A,E=![]() =
=![]() ,
,
∴OE=![]() =
=![]() ,
,
∴A,的坐标为:![]()
故选D.


科目:初中数学 来源: 题型:
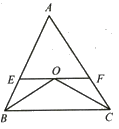
【题目】如图,在△ABC中,∠ABC与∠ACB的平分线相交于O.过点O作EF∥BC分别交AB、AC于E、F.若∠BOC=130°,∠ABC:∠ACB=3:2,求∠AEF和∠EFC.
查看答案和解析>>
科目:初中数学 来源: 题型:
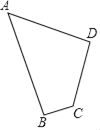
【题目】如图,四边形草坪ABCD中,∠B=90°,AB=24m,BC=7m,CD=15m,AD=20m.
(1)判断∠ADC是否是直角,并说明理由;
(2)试求四边形草坪ABCD的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
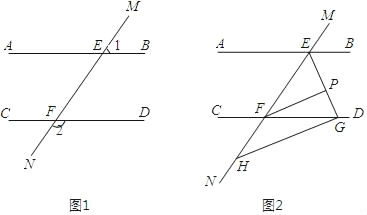
【题目】已知,如图1,直线MN与直线AB、CD分别交于点E、F,∠1与∠2互补.
(1)试判断直线AB与CD的位置关系,并说明理由;
(2)如图2,∠BEF与∠EFD的角平分线交于点P,EP与CD交于点G,点H是MN上的一点且GH⊥EG.求证:PF∥GH.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,我们定义点P(a,b)的“变换点”为Q.且规定:当a≥b时,Q为(b,﹣a);当a<b时,Q为(a,﹣b).
(1)点(2,1)的变换点坐标为;
(2)若点A(a,﹣2)的变换点在函数y= ![]() 的图象上,求a的值;
的图象上,求a的值;
(3)已知直线l与坐标轴交于(6,0),(0,3)两点.将直线l上所有点的变换点组成一个新的图形记作M. 判断抛物线y=x2+c与图形M的交点个数,以及相应的c的取值范围,请直接写出结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,两条射线AM∥BN,线段CD的两个端点C、D分别在射线BN、AM上,且∠A=∠BCD=108°.E是线段AD上一点(不与点A、D重合),且BD平分∠EBC.
(1)求∠ABC的度数.
(2)请在图中找出与∠ABC相等的角,并说明理由.
(3)若平行移动CD,且AD>CD,则∠ADB与∠AEB的度数之比是否随着CD位置的变化而发生变化?若变化,找出变化规律;若不变,求出这个比值.
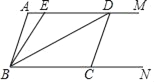
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知△ABC 中,∠ABC=45°,F 是高 AD 和 BE 的交点,∠CAD=30°,CD=4,则线段 BF 的长度为( )
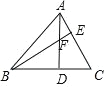
A. 6 B. 7 C. 8 D. 9
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在正方形ABCD和正方形DEFG中,顶点B、D、F在同一直线上,H是BF的中点.
(1)如图1,若AB=1,DG=2,求BH的长;
(2)如图2,连接AH,GH.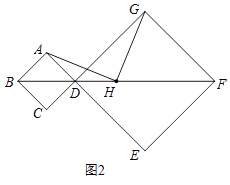
小宇观察图2,提出猜想:AH=GH,AH⊥GH.小宇把这个猜想与同学们进行交流,通过讨论,形成了证明该猜想的几种想法:
想法1:延长AH交EF于点M,连接AG,GM,要证明结论成立只需证△GAM是等腰直角三角形;
想法2:连接AC,GE分别交BF于点M,N,要证明结论成立只需证△AMH≌△HNG.
…
请你参考上面的想法,帮助小宇证明AH=GH,AH⊥GH.(一种方法即可)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com