
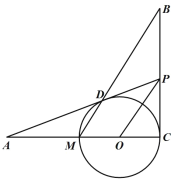
【题目】如图,已知BCAC,圆心O在AC上,点M与点C分别是AC与⊙O的交点,点D是MB与⊙O的交点,点P是AD延长线与BC的交点,且ADAOAMAP,连接OP.
(1)证明:MD//OP;
(2)求证:PD是⊙O的切线;
(3)若AD24,AMMC,求![]() 的值.
的值.
【答案】(1)证明见解析;(2)证明见解析;(3)![]() .
.
【解析】
(1)根据两边成比例夹角相等两三角形相似证明,然后利用平行线的判定定理即可.
(2)欲证明PD是⊙O的切线,只要证明OD⊥PA即可解决问题;
(3)连接CD.由(2)可知:PC=PD,由AM=MC,推出AM=2MO=2R,在Rt△AOD中,![]() ,可得
,可得![]() ,推出
,推出![]() ,推出
,推出![]() ,
,![]() ,由
,由![]() ,可得
,可得![]() ,再利用全等三角形的性质求出MD即可解决问题;
,再利用全等三角形的性质求出MD即可解决问题;
(1)证明:连接![]() 、
、![]() 、
、![]() .
.
∵![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
(2)∴![]() ,
,
∴![]() ,
,![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∵![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() 是
是![]() 的切线.
的切线.
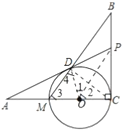
(3)连接![]() .由(1)可知:
.由(1)可知:![]() ,
,
∵![]() ,
,
∴![]() ,
,
在![]() 中,
中,![]() ,
,
∴![]() ,
,
∴![]() ,∴
,∴![]() ,
,![]() ,
,
∵![]() ,
,
∴![]() ,
,
∵![]() 是
是![]() 的中点,
的中点,
∴![]() ,
,
∴点![]() 是
是![]() 的中点,
的中点,
∴![]() ,
,
∵![]() 是
是![]() 的直径,
的直径,
∴![]() ,在
,在![]() 中,
中,
∵![]() ,
,![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() .
.


 备战中考寒假系列答案
备战中考寒假系列答案科目:初中数学 来源: 题型:
【题目】七(2)班共有50名学生,老师安排每人制作一件![]() 型或
型或![]() 型的陶艺品,学校现有甲种制作材料36
型的陶艺品,学校现有甲种制作材料36![]() ,乙种制作材料29
,乙种制作材料29![]() ,制作
,制作![]() 、
、![]() 两种型号的陶艺品用料情况如下表:
两种型号的陶艺品用料情况如下表:
需甲种材料 | 需乙种材料 | |
1件 | 0.9 | 0.3 |
1件 | 0.4 | 1 |
(1)设制作![]() 型陶艺品
型陶艺品![]() 件,求
件,求![]() 的取值范围;
的取值范围;
(2)请你根据学校现有材料,分别写出七(2)班制作![]() 型和
型和![]() 型陶艺品的件数.
型陶艺品的件数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙人5场10次投篮命中次数如图
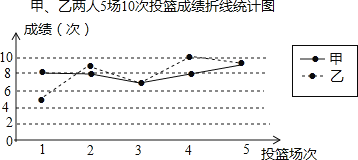
(1)填写表格.
平均数 | 众数 | 中位数 | 方差 | |
甲 | ______ | 8 | 8 | ______ |
乙 | 8 | ______ | ______ | 3.2 |
(2)①教练根据这5个成绩,选择甲参加投篮比赛,理由是什么?
②如果乙再投篮1场,命中8次,那么乙的投监成绩的方差将会怎样变化?(“变大”“变小”或”不变”)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有一边是另一边的![]() 倍的三角形叫做智慧三角形,这两边中较长边称为智慧边,这两边的夹角叫做智慧角.
倍的三角形叫做智慧三角形,这两边中较长边称为智慧边,这两边的夹角叫做智慧角.
(1)已知![]() 为智慧三角形,且
为智慧三角形,且![]() 的一边长为,则该智慧三角形的面积为_________;
的一边长为,则该智慧三角形的面积为_________;
(2)如图①,在![]() 中,
中,![]() ,
,![]() ,求证:
,求证:![]() 是智慧三角形;
是智慧三角形;
(3)如图②,![]() 是智慧三角形,
是智慧三角形,![]() 为智慧边,
为智慧边,![]() 为智慧角,
为智慧角,![]() ,点
,点![]() 在函数
在函数![]() (
(![]() )的图象上,点
)的图象上,点![]() 在点
在点![]() 的上方,且点
的上方,且点![]() 的纵坐标为
的纵坐标为![]() ,当
,当![]() 是直角三角形时,求
是直角三角形时,求![]() 的值.
的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】抛物线![]() (
(![]() 为常数)与
为常数)与![]() 轴交于点
轴交于点![]() 和
和![]() 与
与![]() 轴交于点
轴交于点![]() ,点
,点![]() 为抛物线顶点.
为抛物线顶点.
(Ⅰ)当![]() 时,求点
时,求点![]() ,点
,点![]() 的坐标;
的坐标;
(Ⅱ)①若顶点![]() 在直线
在直线![]() 上时,用含有
上时,用含有![]() 的代数式表示
的代数式表示![]() ;
;
②在①的前提下,当点![]() 的位置最高时,求抛物线的解析式;
的位置最高时,求抛物线的解析式;
(Ⅲ)若![]() ,当
,当![]() 满足
满足![]() 值最小时,求
值最小时,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,D、E分别是AB、AC的中点,BE=2DE,延长DE到点F,使得EF=BE,连接CF.

(1)求证:四边形BCFE是菱形;
(2)若CE=4,∠BCF=120°,求菱形BCFE的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
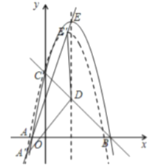
【题目】如图,已知二次函数![]() 的图像与
的图像与![]() 轴交于
轴交于![]() 两点,与
两点,与![]() 轴交于
轴交于![]() ,对称轴为直线
,对称轴为直线![]() ,顶点为
,顶点为![]() .
.
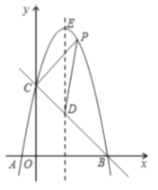
(1)求该二次函数的解析式;
(2)经过![]() 、
、![]() 两点的直线交抛物线的对称轴于点
两点的直线交抛物线的对称轴于点![]() ,点
,点![]() 为直线
为直线![]() 上方抛物线上的一动点,当点
上方抛物线上的一动点,当点![]() 在什么位置时,
在什么位置时,![]() 的面积最大?并求此时点
的面积最大?并求此时点![]() 的坐标及
的坐标及![]() 的最大面积;
的最大面积;
(3)如图,平移抛物线,使抛物线的顶点![]() 在射线
在射线![]() 上移动,点
上移动,点![]() 平移后的对应点为
平移后的对应点为![]() ,点
,点![]() 的对应点为点
的对应点为点![]() ,连接
,连接![]() 、
、![]() ,
,![]() 是否能为等腰三角形?若能,请求出所有符合条件的点
是否能为等腰三角形?若能,请求出所有符合条件的点![]() 的坐标;若不能,请说明理由.
的坐标;若不能,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
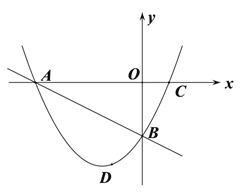
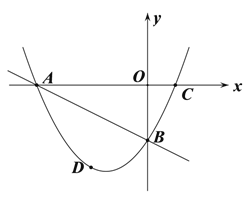
【题目】已知,如图,在平面直角坐标系中,直线![]() 与
与![]() 轴交于点A,与
轴交于点A,与![]() 轴交于点B,抛物线
轴交于点B,抛物线![]() 经过A、B两点,与
经过A、B两点,与![]() 轴的另一个交点为C.
轴的另一个交点为C.
(1)直接写出点A和点B的坐标;
(2)求抛物线的函数解析式;
(3)D为直线AB下方抛物线上一动点;
①连接DO交AB于点E,若DE:OE=3:4,求点D的坐标;
②是否存在点D,使得∠DBA的度数恰好是∠BAC度数2倍,如果存在,求点D 的坐标,如果不存在,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中(如图),已知抛物线
中(如图),已知抛物线![]() 经过点
经过点![]() ,与
,与![]() 轴交于点
轴交于点![]() ,,抛物线的顶点为点
,,抛物线的顶点为点![]() ,对称轴与
,对称轴与![]() 轴交于点
轴交于点![]() .
.

(1)求抛物线的表达式及点![]() 的坐标;
的坐标;
(2)点![]() 是
是![]() 轴正半轴上的一点,如果
轴正半轴上的一点,如果![]() ,求点
,求点![]() 的坐标;
的坐标;
(3)在(2)的条件下,点![]() 是位于
是位于![]() 轴左侧抛物线上的一点,如果
轴左侧抛物线上的一点,如果![]() 是以
是以![]() 为直角边的直角三角形,求点
为直角边的直角三角形,求点![]() 的坐标.
的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com