
【题目】如图,一次函数y=﹣x+b与反比例函数y= ![]() (k≠0)的图象相交于A(﹣1,4)、B(4,﹣1)两点,直线l⊥x轴于点E(﹣4,0),与反比例函数和一次函数的图象分别相交于点C、D,连接AC、BC
(k≠0)的图象相交于A(﹣1,4)、B(4,﹣1)两点,直线l⊥x轴于点E(﹣4,0),与反比例函数和一次函数的图象分别相交于点C、D,连接AC、BC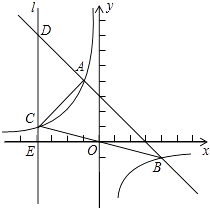
(1)求出b和k;
(2)求证:△ACD是等腰直角三角形;
(3)在y轴上是否存在点P,使S△PBC=S△ABC?若存在,请求出P的坐标;若不存在,请说明理由.
【答案】
(1)解:∵一次函数y=﹣x+b的图象经过点A(﹣1,4)
∴﹣(﹣1)+b=4,
即b=3,
又∵反比例函数y= ![]() (k≠0)的图象经过点A(﹣1,4)
(k≠0)的图象经过点A(﹣1,4)
∴k=xy=(﹣1)×4=﹣4;
(2)证明:∵直线l⊥x轴于点E(﹣4,0)则直线l解析式为x=﹣4,
∴直线x=﹣4与一次函数y=﹣x+3交于点D,则D(﹣4,7)
直线x=﹣4与反比例函数y=﹣ ![]() 交于点C,
交于点C,
则C(﹣4,1)
过点A作AF⊥直线l于点F,
∵A(﹣1,4),C(﹣4,1),D(﹣4,7)
∴CD=6,AF=3,DF=3,FC=3
又∵∠AFD=∠AFC=90°,
由勾股定理得:AC=AD=3 ![]()
又∵AD2+AC2= ![]() =36
=36
CD2=62=36
∴AD2+AC2=CD2
∴由勾股定理逆定理得:△ACD是直角三角形,
又∵AD=AC
∴△ACD是等腰直角三角形;
(3)解:过点A作AP1∥BC,交y轴于P1,
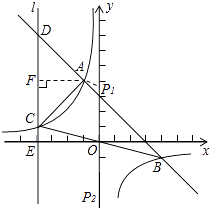
则S△PBC=S△ABC
∵B(4,﹣1),C(﹣4,1)
∴直线BC的解析式为y=﹣ ![]() x
x
∵设直线AP1的解析式为y=﹣ ![]() x+b1,把A(﹣1,4)代入可求b1=
x+b1,把A(﹣1,4)代入可求b1= ![]() ,
,
∴P1(0, ![]() ),
),
∴作P1关于x轴的对称点P2,则 ![]() =S△ABC,
=S△ABC,
故P2(0,﹣ ![]() );
);
即存在P1(0, ![]() ),P2(0,﹣
),P2(0,﹣ ![]() );
);
【解析】(1)利用待定系数法即可求解。
(2)根据已知及点E的坐标易求出点C、D的坐标,因此可求出DC的长,过点A作AF⊥直线l于点F,即可求出AF,DF,FC的长,根据垂直平分线的性质得出AC=AD,然后再证明△ACD是直角三角形,即可得出结论。
(3)先求出直线BC的函数解析式,再求出直线AP1的解析式,就可求出点P1的坐标。作P1关于x轴的对称点P2,则S △ P 1 B C = S △ P 2 B C=S△ABC,,就可求出点P2的坐标。
【考点精析】认真审题,首先需要了解等腰直角三角形(等腰直角三角形是两条直角边相等的直角三角形;等腰直角三角形的两个底角相等且等于45°),还要掌握确定一次函数的表达式(确定一个一次函数,需要确定一次函数定义式y=kx+b(k不等于0)中的常数k和b.解这类问题的一般方法是待定系数法)的相关知识才是答题的关键.


科目:初中数学 来源: 题型:
【题目】如图,以直角三角形AOC的直角顶点O为原点,以OC、OA所在直线为x轴和y轴建立平面直角坐标系,点A(0,a),C(b,0)满足![]() .D为线段AC的中点.在平面直角坐标系中,以任意两点P(x1,y1)、Q(x2,y2)为端点的线段中点坐标为
.D为线段AC的中点.在平面直角坐标系中,以任意两点P(x1,y1)、Q(x2,y2)为端点的线段中点坐标为![]() ,
,![]() .
.

(1)则A点的坐标为 ;点C的坐标为 .D点的坐标为 .
(2)已知坐标轴上有两动点P、Q同时出发,P点从C点出发沿x轴负方向以1个单位长度每秒的速度匀速移动,Q点从O点出发以2个单位长度每秒的速度沿y轴正方向移动,点Q到达A点整个运动随之结束.设运动时间为t(t>0)秒.问:是否存在这样的t,使S△ODP=S△ODQ,若存在,请求出t的值;若不存在,请说明理由.
(3)点F是线段AC上一点,满足∠FOC=∠FCO,点G是第二象限中一点,连OG,使得∠AOG=∠AOF.点E是线段OA上一动点,连CE交OF于点H,当点E在线段OA上运动的过程中,![]() 的值是否会发生变化?若不变,请求出它的值;若变化,请说明理由.
的值是否会发生变化?若不变,请求出它的值;若变化,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】探究:
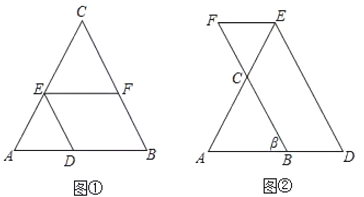
(1)如图①,在![]() 中,点
中,点![]() 、
、![]() 、
、![]() 分别在边
分别在边![]() 、
、![]() 、
、![]() 上,且
上,且![]() ,若
,若![]() ,求
,求![]() 的度数.请将下面的解答过程补充完整,并填空.
的度数.请将下面的解答过程补充完整,并填空.
(1)解:
![]() ,
,
![]() (两直线平行,内错角相等).
(两直线平行,内错角相等).
![]() ,
,
![]() (___________________________________).
(___________________________________).
![]() (__________________).
(__________________).
![]() .
.
应用:
(2)如图②,在![]() 中,点
中,点![]() 、
、![]() 、
、![]() 分别在边
分别在边![]() 、
、![]() 、
、![]() 的延长线上,且
的延长线上,且![]() ,
,![]() ,若
,若,求
![]() 的大小.(用含
的大小.(用含![]() 的代数式表示).
的代数式表示).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD中,AB=CD,对角线AC,BD相交于点O,AE⊥BD于点E,CF⊥BD于点F,连接AF,CE,若DE=BF,则下列结论:①CF=AE;②OE=OF;③四边形ABCD是平行四边形;④图中共有四对全等三角形.其中正确结论的个数是

A.4 B.3 C.2 D.1
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,动点P在平面直角坐标系中按图中箭头所示方向运动,第1次从原点运动到点(1,1),第2次接着运动到点(2,0),第3次接着运动到点(3,2),…,按这样的运动规律,经过第2017次运动后,动点P的坐标是______.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小颖和小红两位同学在学习“概率”时,做投掷骰子(质地均匀的正方体)试验,她们共做了60次试验,试验的结果如下:
朝上的点数 | 1 | 2 | 3 | 4 | 5 | 6 |
出现的次数 | 7 | 9 | 6 | 8 | 20 | 10 |
(1)计算“3点朝上”的频率和“5点朝上”的频率.
(2)小颖说:“根据上述试验,一次试验中出现5点朝上的概率最大”;小红说:“如果投掷600次,那么出现6点朝上的次数正好是100次”.小颖和小红的说法正确吗?为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法正确的有( )
①绝对值等于本身的数是正数;②将数60340精确到千位是![]() ③连接两点的线段的长度就是两点间的距离;④若AC=BC,则点C就是线段AB的中点.
③连接两点的线段的长度就是两点间的距离;④若AC=BC,则点C就是线段AB的中点.
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,AC∥DF,直线AF分别直线BD、CE 相交于点G、H,∠1=∠2,
求证:∠C=∠D.
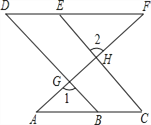
证明: ∵∠1=∠2(已知)
∠1=∠DGH( ),
∴∠2=__________( 等量代换 )
∴__________∥__________( 同位角相等,两直线平行 )
∴∠C=___________( 两直线平行,同位角相等 )
又∵AC∥DF__________
∴∠D=∠ABG_________
∴∠C=∠D__________
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com