
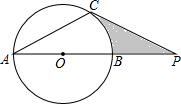
 已知如图,⊙O的直径AB与弦AC的夹角∠A=30°,AC=CP.
已知如图,⊙O的直径AB与弦AC的夹角∠A=30°,AC=CP.分析 (1)如图,连接OC;运用已知条件证明∠OCP=90°,即可解决问题.
(2)分别求出△OCP、扇形OCB的面积,即可解决问题.
解答 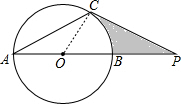 解:(1)如图,连接OC;
解:(1)如图,连接OC;
∵OA=OC,AC=CP,
∴∠A=∠OCA=30°,∠P=∠A=30°,
∴∠POC=∠A+∠OCA=60°,
∴∠OCP=180°-60°-30°=90°,
∴CP是⊙O的切线.
(2)∵AB=4$\sqrt{3}$,
∴OC=OB=2$\sqrt{3}$,
∴PC=$\frac{OC}{tan30°}$=6
∴S△OCP=$\frac{1}{2}$OC•PC
=$\frac{1}{2}$×2$\sqrt{3}$•6=6$\sqrt{3}$,
S扇形OBC=$\frac{60π•(2\sqrt{3})^{2}}{360}$=2π,
∴图中阴影部分的面积=6$\sqrt{3}$-2π.
点评 该题主要考查了切线的判定、三角形的面积公式、扇形的面积公式等几何知识点及其应用问题;解题的方法是作辅助线;解题的关键是准确选择切线的判定方法;灵活运用扇形的面积公式等几何知识点来分析、判断、解答.


 小学同步三练核心密卷系列答案
小学同步三练核心密卷系列答案科目:初中数学 来源: 题型:解答题
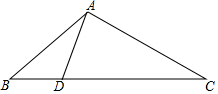 如图,将①∠BAD=∠C;②∠ADB=∠CAB;③AB2=BD•BC;④$\frac{CA}{AD}$=$\frac{AB}{DB}$;⑤$\frac{BC}{BA}$=$\frac{DA}{AC}$中的一个作为条件,另一个作为结论,组成一个真命题.
如图,将①∠BAD=∠C;②∠ADB=∠CAB;③AB2=BD•BC;④$\frac{CA}{AD}$=$\frac{AB}{DB}$;⑤$\frac{BC}{BA}$=$\frac{DA}{AC}$中的一个作为条件,另一个作为结论,组成一个真命题.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com