
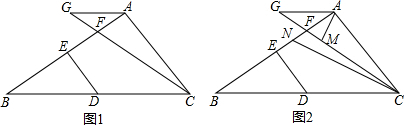
分析 (1)根据平行线的判定和性质可得∠GAC+∠ACB=180°,根据等量关系可得∠EDB=∠ACB,根据平行线的判定和性质可得AB⊥AC.
(2)根据余角的性质可得∠MAB=∠ACN,根据三角形外角的性质、角平分线的性质和平行线的性质可得∠AGC的度数.
解答 解:(1)∵∠GAB=∠B,
∴GA∥BC,
∴∠GAC+∠ACB=180°,
∵∠GAC+∠EDB=180°,
∴∠EDB=∠ACB,
∴ED∥AC,
∵DE⊥AB,
∴AB⊥AC.
(2)∵∠GAC的平分线交CG于点M,∠ACB的平分线交AB于点N,
∴∠ACN+∠MAC=$\frac{1}{2}$×180°=90°,
∵∠MAB+∠MAC=∠ACN+∠MAC=90°,
∴∠MAB=∠ACN=∠NCB,
∵∠AMC-∠ANC=35°,
∴∠BAM+∠NCG=∠BCG=35°,
∵GA∥BC,
∴∠AGC=35°.
点评 本题考查的是三角形的内角和定理,平行线的判定与性质,三角形外角的性质、角平分线的性质掌握三角形内角和等于180°是解题的关键.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:填空题
 已知:如图,在△ABC,△ADE中,∠BAC=∠DAE=90°,AB=AC,AD=AE,点C,D,E三点在同一条直线上,连接BD,BE.则下列结论中正确的是:①②③④.①BD=CE;②BD⊥CE;③∠ACE+∠DBC=45°;④∠BAE+∠DAC=180°.(把所有正确结论的序号都填在横线上)
已知:如图,在△ABC,△ADE中,∠BAC=∠DAE=90°,AB=AC,AD=AE,点C,D,E三点在同一条直线上,连接BD,BE.则下列结论中正确的是:①②③④.①BD=CE;②BD⊥CE;③∠ACE+∠DBC=45°;④∠BAE+∠DAC=180°.(把所有正确结论的序号都填在横线上)查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 3b3-(2ab2-4a2b+a3) | B. | 3b3-(2ab2+4a2b+a3) | ||
| C. | 3b3-(-2ab2+4a2b-a3) | D. | 3b3-(2ab2+4a2b-a3) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com