
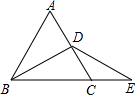
 如图,C是BE上一点,D是AC的中点,且AB=AC,DE=DB,∠A=60°,△ABC的周长是18cm.求∠E的度数及CE的长度.
如图,C是BE上一点,D是AC的中点,且AB=AC,DE=DB,∠A=60°,△ABC的周长是18cm.求∠E的度数及CE的长度. 分析 根据有一个角是60°的等腰三角形是等边三角形得:△ABC是等边三角形,由此可计算边长为6cm,根据等腰三角形三线合一的性质得中线AD是高线和角平分线,所以可以求得CD的长,由外角定理证明∠CDE=∠E,所以CE=CD=3cm.
解答 解:∵AB=AC,∠A=60°,
∴△ABC是等边三角形,
∴AC=BC=AB,∠ABC=∠ACB=∠A=60°,
∵△ABC的周长是18cm,
∴AB=AC=BC=$\frac{1}{3}$×18=6cm,
∵D是AC的中点,
∴CD=$\frac{1}{2}$AC=$\frac{1}{2}$×6=3cm,
∵AB=BC,D是AC的中点,
∴∠CBD=$\frac{1}{2}$∠ABC=$\frac{1}{2}$×60°=30°,
∵BD=DE,
∴∠CBD=∠E=30°,
∵∠ACB是△DCE的一个外角,
∴∠ACB=∠E+∠CDE,
∴∠CDE=60°-30°=30°,
∴∠CDE=∠E,
∴CE=CD=3cm.
点评 本题考查了等腰三角形和等边三角形的性质和判定,是常考题型,难度不大;要熟练掌握等腰三角形三线合一的性质:等腰三角形的顶角平分线、底边上的中线、底边上的高相互重合;熟记由等腰三角形来判定等边三角形常用的判定方法:有一个角是60°的等腰三角形是等边三角形.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 1 | ● | ○ | x | 7 | -3 | … |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 1个 | B. | 2 个 | C. | 3 个 | D. | 4 个 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
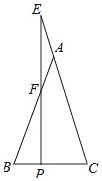 如图,在△ABC中,AB=AC,点E在CA延长线上,EP⊥BC于点P,交AB于点F.
如图,在△ABC中,AB=AC,点E在CA延长线上,EP⊥BC于点P,交AB于点F.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
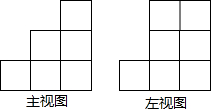 如图是由一些大小相同的小正方体组成的简单几何体的主视图和左视图.若组成这个几何体的小正方体的块数为n,请你写出n的所有可能值并画出每一个N的取值的一种几何体的俯视图.
如图是由一些大小相同的小正方体组成的简单几何体的主视图和左视图.若组成这个几何体的小正方体的块数为n,请你写出n的所有可能值并画出每一个N的取值的一种几何体的俯视图.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com