
如图,直线 与x轴、y 轴分别交于点A 和点B,点C在直线AB上,且点C的纵坐标为一1,点D 在反比例函数
与x轴、y 轴分别交于点A 和点B,点C在直线AB上,且点C的纵坐标为一1,点D 在反比例函数 的图象上,CD平行于y轴,
的图象上,CD平行于y轴, ,则k的值为 。
,则k的值为 。
3
解析试题分析:把x=2代入 求出C的纵坐标,得出OM=2,CM=1,根据CD∥y轴得出D的横坐标是2,根据三角形的面积求出CD的值,求出MD,得出D的纵坐标,把D的坐标代入反比例函数的解析式求出k即可.
求出C的纵坐标,得出OM=2,CM=1,根据CD∥y轴得出D的横坐标是2,根据三角形的面积求出CD的值,求出MD,得出D的纵坐标,把D的坐标代入反比例函数的解析式求出k即可.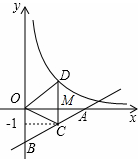
∵点C在直线AB上,即在直线 上,点C的纵坐标为-1,
上,点C的纵坐标为-1,
∴代入得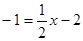 ,解得,x=2,即C(2,-1),
,解得,x=2,即C(2,-1),
∴OM=2,
∵CD∥y轴,S△OCD=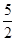 ,
,
∴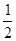 CD×OM=
CD×OM=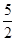 ,
,
∴CD=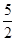 ,
,
∴MD=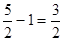 ,
,
即D的坐标是(2,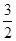 ),
),
∵D在双曲线 上,
上,
∴代入得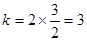 .
.
考点:反比例函数与一次函数的交点问题,一次函数、反比例函数的图象上点的坐标特征,三角形的面积公式
点评:通过做此题培养了学生的计算能力和理解能力,题目具有一定的代表性,是一道比较好的题目.


科目:初中数学 来源: 题型:
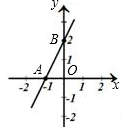 如图,直线与x轴、y轴分别交于A、B两点.
如图,直线与x轴、y轴分别交于A、B两点.查看答案和解析>>
科目:初中数学 来源: 题型:
| 1 |
| 2x |
| 1 |
| 2x |
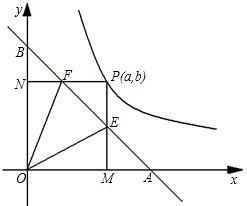
查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,直线与x轴、y轴分别交于A、B两点.
如图,直线与x轴、y轴分别交于A、B两点.查看答案和解析>>
科目:初中数学 来源:2011届宁夏银川市初三上学期期末数学卷 题型:解答题
如图①,直线 与x轴、y轴分别交于B、C两点,点A在x轴负半轴上,且
与x轴、y轴分别交于B、C两点,点A在x轴负半轴上,且 ,抛物线经过A、B、C三点,D为线段AB中点,点P(m,n)是该抛物线上的一个动点(其中m>0,n<0),连接DP交BC于点E.
,抛物线经过A、B、C三点,D为线段AB中点,点P(m,n)是该抛物线上的一个动点(其中m>0,n<0),连接DP交BC于点E.
(1)写出A、B、C三点的坐标,并求抛物线的解析式;(5分)
(2) 当△BDE是等腰三角形时,直接写出此时点E的坐标;(3分)
(3)连结PC、PB,△PBC是否有最大面积?若有,求出△PBC的最大面积和此时P点的坐标;若没有,请说明理由。(3分)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com