
已知:如图, AB是⊙O的直径,AM和BN是⊙O的两条切线,点D是AM上一点,联结OD , 作BE∥OD交⊙O于点E, 联结DE并延长交BN于点C.
(1)求证:DC是⊙O的切线;
(2)若AD=l,BC=4,求直径AB的长.

(1)证明见解析;(2)4.
【解析】
试题分析:(1)连接OE,由OE=OB,利用等边对等角得到一对角相等,再由OD与BE平行,得到一对同位角及一对内错角相等,等量代换得到∠AOD=∠OBE=∠OEB=∠EOD,再由OA=OE,OD=OD,利用SAS得到三角形AOD与三角形EOD全等,由全等三角形对应角相等得到∠OAD=∠OED,根据AM为圆O的切线,利用切线的性质得到∠OAD=∠OED=90°,即可得证.
(2)过点D作BC的垂线,垂足为H,由BN与圆O切线于点B,得到∠ABC=90°=∠BAD=∠BHD,利用三个角为直角的四边形为矩形得到ADHB为矩形,利用矩形的对边相等得到BH=AD=1,AB=DH,由BC-BH求出HC的长,AD、CB、CD分别切⊙O于点A、B、E,利用切线长定理得到AD=DE=1,EC=BC=4,在直角三角形DHC中,利用勾股定理求出DH的长,即为AB的长.
试题解析:(1)如图,连接OE,
在⊙O中,OA=OE=OB,∴∠OBE=∠OEB.
∵OD∥BE,∴∠AOD=∠OBE=∠OEB=∠EOD.
在△AOD和△EOD中,OA=OE,∠AOD=∠EOD,OD=OD,
∴△AOD≌△EOD(SAS).∴∠OAD=∠OED.
∵AM是⊙O的切线,切点为A,∴BA⊥AM.
∴∠OAD=∠OED=90°.∴OE⊥DE.
∵OE是⊙O的半径,∴DE是⊙O的切线.
(2)如图,过点D作BC的垂线,垂足为H,
∵BN切⊙O于点B,∴∠ABC=90°=∠BAD=∠BHD.∴四边形ABHD是矩形.
∴AD=BH=1,AB=DH,∴CH=BC-BH=4-1=3.
∵AD、CB、CD分别切⊙O于点A、B、E,∴AD=ED=1,BC=CE=4.
∴DC=DE+CE=1+4=5,
在Rt△DHC中,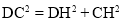 ,
,
∴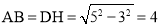 .
.

考点:1.切线的判定和性质;2.全等三角形的判定和性质;3.勾股定理,4.等腰三角形的性质;5.平行的性质;6.矩形的判定和性质.


科目:初中数学 来源:2013-2014学年北京市昌平区中考一模数学试卷(解析版) 题型:解答题
无论k取任何实数,对于直线 都会经过一个固定的点
都会经过一个固定的点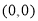 ,我们就称直线
,我们就称直线 恒过定点
恒过定点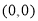 .
.
(1)无论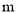 取任何实数,抛物线
取任何实数,抛物线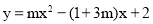 恒过定点
恒过定点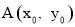 ,直接写出定点A的坐标;
,直接写出定点A的坐标;
(2)已知△ABC的一个顶点是(1)中的定点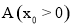 ,且∠B,∠C的角平分线分别是y轴和直线
,且∠B,∠C的角平分线分别是y轴和直线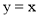 ,求边BC所在直线的表达式;
,求边BC所在直线的表达式;
(3)求△ABC内切圆的半径.
查看答案和解析>>
科目:初中数学 来源:2013-2014学年北京市昌平区中考一模数学试卷(解析版) 题型:选择题
如图,在△ABC中,AB=AC,tan∠B=2, BC=3 . 边AB上一动点M从点B出发沿B→A运动,动点N从点B出发沿B→C→A运动,在运动过程中,射线MN与射线BC交于点E,且夹角始终保持45°. 设BE=x, MN=y,则能表示y与x的函数关系的大致图象是( )
. 边AB上一动点M从点B出发沿B→A运动,动点N从点B出发沿B→C→A运动,在运动过程中,射线MN与射线BC交于点E,且夹角始终保持45°. 设BE=x, MN=y,则能表示y与x的函数关系的大致图象是( )

A.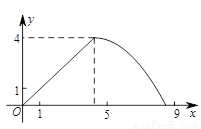
B. 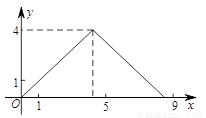
C. 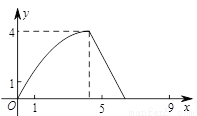
D. 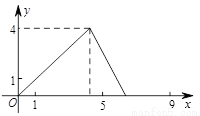
查看答案和解析>>
科目:初中数学 来源:2013-2014学年北京市昌平区中考一模数学试卷(解析版) 题型:选择题
据统计,第22届冬季奥林匹克运动会的电视转播时间长达88000小时,社交网站和国际奥委会官方网站也创下冬奥会收看率纪录. 用科学计数法表示88000为( )
A.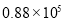 B.
B.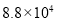 C.
C.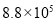 D.
D.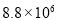
查看答案和解析>>
科目:初中数学 来源:2013-2014学年北京市丰台区中考二模数学卷(解析版) 题型:解答题
某产品生产车间有工人10名.已知每名工人每天可生产甲种产品12个或乙种产品10个,且每生产一个甲种产品可获利润100元,每生产一个乙种产品可获利润180元.在这10名工人中,如果要使此车间每天所获利润不低于15600元,你认为至少要派多少名工人去生产乙种产品才合适.
查看答案和解析>>
科目:初中数学 来源:2013-2014学年内蒙古九年级6月中考模拟数学试卷(解析版) 题型:解答题
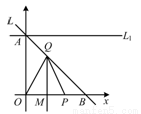
如图,已知直线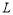 过点
过点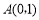 和
和 ,
,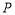 是
是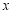 轴正半轴上的动点,
轴正半轴上的动点,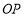 的垂直平分线交
的垂直平分线交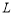 于点
于点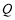 ,交
,交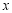 轴于点
轴于点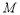 .
.
(1)直接写出直线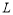 的解析式;
的解析式;
(2)当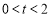 时,设
时,设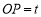 ,
,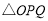 的面积为
的面积为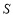 ,求S关于t的函数关系式;并求出S的最大值;
,求S关于t的函数关系式;并求出S的最大值;
(3)当点Q在线段AB上(Q与A、B不重合)时,直线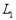 过点A且与x轴平行,问在
过点A且与x轴平行,问在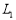 上是否存在点C,使得
上是否存在点C,使得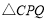 是以
是以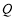 为直角顶点的等腰直角三角形?若存在,求出点C的坐标,并证明;若不存在,请说明理由.
为直角顶点的等腰直角三角形?若存在,求出点C的坐标,并证明;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com