
【题目】如图所示,已知∠1+∠2=180°,∠3=∠B,
求证:∠AED=∠ACB.

证明:∠1+∠2=180°(已知),∠1+∠4=180°( ),
∴∠2= ( ),
∴AB∥EF( ),
∴∠3= ( ),
∵∠3=∠B(已知),
∴∠B= (等量代换),
∴DE∥BC( ),
∴∠AED=∠ACB( ).
 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,二次函数y=ax2+bx+c(a≠0)的图象的顶点在第一象限,且过点(0,1)和(-1,0).下列结论:①ab<0;②b2>4a;③0<a+b+c<2;④0<b<1;⑤当x>-1时,y>0.其中正确结论的个数是( )
A.5个
B.4个
C.3个
D.2个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读材料,回答问题:
若整数![]() 能被4整除,则称整数
能被4整除,则称整数![]() 为“完美数”.例如:8能被4整除,所以8是“完美数”;一4是4的倍数,所以一4也是“完美数”。
为“完美数”.例如:8能被4整除,所以8是“完美数”;一4是4的倍数,所以一4也是“完美数”。
(1)10到15之间的“完美数”是_______;
若![]() ,
,![]() 是整数,则
是整数,则![]() ________ “完美数”(填:“是”或“不是”);
________ “完美数”(填:“是”或“不是”);
(2)若任意四个连续的“完美数”中最小数的是4![]() (
(![]() 是整数),则它与四个数中最大数的积是32的倍数吗?请说明理由;
是整数),则它与四个数中最大数的积是32的倍数吗?请说明理由;
(3)当![]() 是正整数时,试说明:
是正整数时,试说明:![]() 一定是“完美数”.
一定是“完美数”.
查看答案和解析>>
科目:初中数学 来源: 题型:
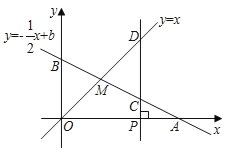
【题目】如图,已知函数![]() 的图象与
的图象与![]() 轴、
轴、![]() 轴分别交于点
轴分别交于点![]() ,与函数
,与函数![]() 的图象交于点
的图象交于点![]() ,点
,点![]() 的横坐标为2.在
的横坐标为2.在![]() 轴上有一点
轴上有一点![]() (其中
(其中![]() ),过点
),过点![]() 作
作![]() 轴的垂线,分别交函数
轴的垂线,分别交函数![]() 和
和![]() 的图象于点
的图象于点![]() .
.
(1)求点![]() 的坐标;
的坐标;
(2)若四边形![]() 是平行四边形,求
是平行四边形,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,已知线段AB、CD相交于点O,连接AC、BD,我们把形如图①的图形称之为“8字形”.
(1)如图①,若∠A=∠D,判断∠C与∠B的数量关系,并说明理由;
(2)如图②,∠CAB和∠BDC的平分线AP和DP相交于点P,并且与CD、AB分别相交于M、N,试解答下列问题:
①仔细观察,在图②中有 个“8字形”;
②∠B=80°,∠C=100°,求∠P的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,某社会实践活动小组实地测量两岸互相平行的一段河的宽度,在河的南岸边点A处,测得河的北岸边点B在其北偏东45°方向,然后向西走60m到达C点,测得点B在点C的北偏东60°方向,如图2.
(1)求∠CBA的度数.
(2)求出这段河的宽(结果精确到1m,备用数据 ![]() ≈1.41,
≈1.41, ![]() ≈1.73).
≈1.73).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,排球运动员站在点O处练习发球,将球从D点正上方2m的A处发出,把球看成点,其运行的高度y(m)与运行的水平距离x(m)满足关系式y=a(x﹣k)2+h.已知球与D点的水平距离为6m时,达到最高2.6m,球网与D点的水平距离为9m.高度为2.43m,球场的边界距O点的水平距离为18m,则下列判断正确的是( )
A.球不会过网
B.球会过球网但不会出界
C.球会过球网并会出界
D.无法确定
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,点H是BC的中点,作射线AH,在线段AH及其延长线上分别取点E,F,连结BE,CF.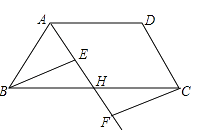
(1)请你添加一个条件,使得△BEH≌△CFH,你添加的条件是,并证明.
(2)在问题(1)中,当BH与EH满足什么关系时,四边形BFCE是矩形,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(背景知识)研究平面直角坐标系,我们可以发现一条重要的规律:若平面直角坐标系上有两个不同的点![]() 、
、![]() ,则线段AB的中点坐标可以表示为
,则线段AB的中点坐标可以表示为![]()

(简单应用)如图1,直线AB与y轴交于点![]() ,与x轴交于点
,与x轴交于点![]() ,过原点O的直线L将
,过原点O的直线L将![]() 分成面积相等的两部分,请求出直线L的解析式;
分成面积相等的两部分,请求出直线L的解析式;
(探究升级)小明发现“若四边形一条对角线平分四边形的面积,则这条对角线必经过另一条对角线的中点”
如图2,在四边形ABCD中,对角线AC、BD相交于点O,![]() 试说明
试说明![]() ;
;
(综合运用)如图3,在平面直角坐标系中![]() ,
,![]() ,
,![]() ,若OC恰好平分四边形OACB的面积,求点C的坐标.
,若OC恰好平分四边形OACB的面积,求点C的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com