
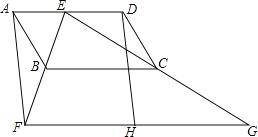
【题目】如图,四边形ABCD为平行四边形,E为AD上的一点,连接EB并延长,使![]() ,连接EC并延长,使
,连接EC并延长,使![]() ,连接
,连接![]() 为FG的中点,连接DH.
为FG的中点,连接DH.
![]() 求证:四边形AFHD为平行四边形;
求证:四边形AFHD为平行四边形;
![]() 若
若![]() ,
,![]() ,
,![]() ,求
,求![]() 的度数.
的度数.
科目:初中数学 来源: 题型:
【题目】德国科学家贝塞尔推算出天鹅座第![]() 颗暗星距地球
颗暗星距地球![]() ,比太阳到地球的距离还远
,比太阳到地球的距离还远![]() 倍.
倍.
![]() 用科学记数法表示出暗星到地球的距离;
用科学记数法表示出暗星到地球的距离;
![]() 用科学记数法表示出
用科学记数法表示出![]() 这个数;
这个数;
![]() 如果光的速度大约是
如果光的速度大约是![]() ,那么你能计算出从暗星发出的光线到地球需要多少秒吗?用科学记数法表示出来.
,那么你能计算出从暗星发出的光线到地球需要多少秒吗?用科学记数法表示出来.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在四边形![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 是
是![]() 上一点,
上一点,![]() 是
是![]() 延长线上一点,且
延长线上一点,且![]() .
.
(1)在图1中,求证:![]() .
.
(2)在图1中,若点![]() 在
在![]() 上且
上且![]() ,试猜想
,试猜想![]() 、
、![]() 、
、![]() 之间的数量关系并证明.
之间的数量关系并证明.
(3)运用(1)(2)解答中所积累的经验知识,完成下题:如图2,在四边形![]() 中,
中,![]() ,
,![]() ,
,![]() 在
在![]() 上,
上,![]() ,且
,且![]() ,若
,若![]() ,求
,求![]() 的长.
的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在甲、乙两个不透明的布袋里,都装有3个大小、材质完全相同的小球,其中甲袋中的小球上分别标有数字0,1,2;乙袋中的小球上分别标有数字﹣1,﹣2,0.现从甲袋中任意摸出一个小球,记其标有的数字为x,再从乙袋中任意摸出一个小球,记其标有的数字为y,以此确定点M的坐标(x,y).
(1)请你用画树状图或列表的方法,写出点M所有可能的坐标;
(2)求点M(x,y)在函数y=﹣ ![]() 的图象上的概率.
的图象上的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下列材料,然后解答后面的问题。
我们知道方程![]() 有无数组解,但在实际生活中我们往往只需要求出其正整数解。例:由
有无数组解,但在实际生活中我们往往只需要求出其正整数解。例:由![]() ,得
,得![]() ,(
,( ![]() 、
、![]() 为正整数)
为正整数)
![]() 则有
则有![]() .又
.又![]() 为正整数,则
为正整数,则![]() 为整数.
为整数.
由2与3互质,可知: ![]() 为3的倍数,从而
为3的倍数,从而![]() ,代入
,代入![]() .
.
![]() 的正整数解为
的正整数解为![]()
问题:(1)若![]() 为自然数,则满足条件的
为自然数,则满足条件的![]() 值有_____________个
值有_____________个
(2)请你写出方程![]() 的所有正整数解:_________________________
的所有正整数解:_________________________
(3)若![]() ,请用含
,请用含![]() 的式子表示
的式子表示![]() ,并求出它的所有整数解。
,并求出它的所有整数解。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一透明的敞口正方体容器ABCD﹣A′B′C′D′装有一些液体,棱AB始终在水平桌面上,容器底部的倾斜角为α(∠CBE=α,如图1所示).探究 如图1,液面刚好过棱CD,并与棱BB′交于点Q,此时液体的形状为直三棱柱,其三视图及尺寸如图2所示.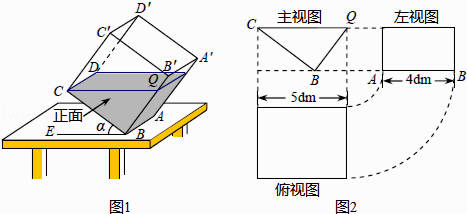
解决问题:
(1)CQ与BE的位置关系是 , BQ的长是dm;
(2)求液体的体积;(参考算法:直棱柱体积V液=底面积S△BCQ×高AB)
(3)求α的度数.(注:sin49°=cos41°= ![]() ,tan37°=
,tan37°= ![]() )
)
(4)延伸:在图4的基础上,于容器底部正中间位置,嵌入一平行于侧面的长方形隔板(厚度忽略不计),得到图5,隔板高NM=1dm,BM=CM,NM⊥BC.继续向右缓慢旋转,当α=60°时,通过计算,判断溢出容器的液体能否达到4dm3 . 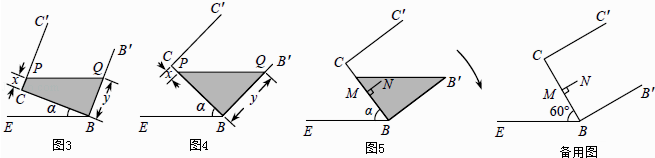
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正六边形ABCDEF的边长为6cm,P是对角线BE上一动点,过点P作直线l与BE垂直,动点P从B点出发且以1cm/s的速度匀速平移至E点.设直线l扫过正六边形ABCDEF区域的面积为S(cm2),点P的运动时间为t(s),下列能反映S与t之间函数关系的大致图象是( )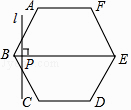
A.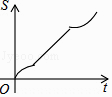
B.
C.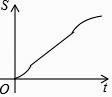
D.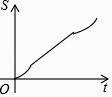
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com