练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    13．给出正三角形、正方形、正五边形、正六边形四种形状的地砖，若只能选购其中的一种地砖来铺满地面，则可供选择的地砖共有（　　）
    A．4种B．3种C．2种D．1种

    分析 由镶嵌的条件知，判断一种图形是否能够镶嵌，只要看一看正多边形的内角度数是否能整除360°，能整除的可以平面镶嵌，反之则不能．

    解答 解：正三角形的每个内角是60°，能整除360°，6个能组成镶嵌；
    正方形的每个内角是90°，4个能组成镶嵌；
    正五边形每个内角是180°-360°÷5=108°，不能整除360°，不能镶嵌；
    正六边形的每个内角是120°，能整除360°，3个能组成镶嵌；
    故若只能选购其中的一种地砖来铺满地面，则可供选择的地砖共有3种．
    故选B．

    点评 此题主要考查了平面镶嵌，用一种正多边形的镶嵌应符合一个内角度数能整除360°．任意多边形能进行镶嵌，说明它的内角和应能整除360°．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：选择题

    3．一次函数y=-2x-3的图象与y轴的交点坐标是（　　）
    A．（3，0）B．（0，3）C．（-3，0）D．（0，-3）

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

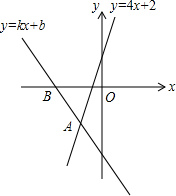    4．如图，经过点B（-2，0）的直线y=kx+b与直线y=kx+b相交于点A（-1，-2），则不等式4x+2＜kx+b＜0的解集为（　　）
    A．-2＜x＜-1B．-2$＜x＜-\frac{1}{2}$C．-1$＜x＜-\frac{1}{2}$D．-$\frac{1}{2}＜x＜0$

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    1．如图，把△ABC向上平移3个单位长度，再向右平移2个单位长度，得到△A′B′C′．
    （1）画出△A′B′C′；
    （2）若点P（m，n）是△ABC某边上的点，经上述平移后，点P的对应点为P′，写出点P′的坐标；
    （3）连接A′A，C′C，求四边形A′ACC′的面积．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

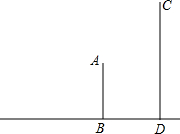    8．已知如图，从20米高的甲楼A望乙楼顶C处的仰角是30°，望乙楼底D处的俯角是45°，求乙楼的高度（精确到0.1米，$\sqrt{2}$≈1.414，$\sqrt{3}$≈1.732）．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    18．若am=2，an=3，则am+n的值为（　　）
    A．5B．6C．8D．9

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    5．某校八年级共有四个班，各班的人数如图1所示，人数比例如图2所示．
    （1）试求出该校八年级的学生总人数；
    （2）请补充条形统计表；
    （3）在一次数学考试中，1班、2班、3班、4班的平均成绩分别为92分、91分、90分、95分．试求出该校八年级学生在本次数学考试的平均分．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

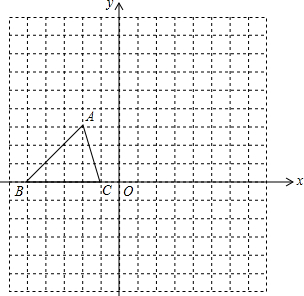    2．如图所示，已知△ABC的三个顶点的坐标分别为A（-2，3）、B（-6，0）、C（-1，0）．
    （1）将△ABC向右平移6个单位长度，在图中画出平移后的△A1B1C1；
    （2）写出△A1B1C1各顶点的坐标；
    （3）求出四边形ABB1A1的面积．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    3．已知：如图所示，E为正方形ABCD外一点，AE=AD，∠ADE=75°，求∠AEB的度数．

    查看答案和解析>>

    同步练习册答案