
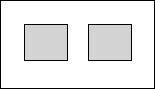
 某广场绿化工程中有一块长2千米,宽1千米的矩形空地,计划在其中修建两块相同的矩形绿地,两块绿地之间既周边留有宽度相等的人行通道(如图),并在这些人行通道铺上瓷砖,要求铺瓷砖的面积是矩形空地面积的$\frac{1}{2}$,设人行通道的宽度为x千米,则下列方程正确的是( )
某广场绿化工程中有一块长2千米,宽1千米的矩形空地,计划在其中修建两块相同的矩形绿地,两块绿地之间既周边留有宽度相等的人行通道(如图),并在这些人行通道铺上瓷砖,要求铺瓷砖的面积是矩形空地面积的$\frac{1}{2}$,设人行通道的宽度为x千米,则下列方程正确的是( )| A. | (2-3x)(1-2x)=1 | B. | $\frac{1}{2}$(2-3x)(1-2x)=1 | C. | $\frac{1}{4}$(2-3x)(1-2x)=1 | D. | $\frac{1}{4}$(2-3x)(1-2x)=2 |
 走进文言文系列答案
走进文言文系列答案科目:初中数学 来源: 题型:解答题
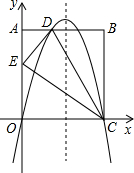 如图,在矩形OABC中,AO=10,AB=8,沿直线CD折叠矩形OABC的一边BC,使点B落在OA边上的点E处,分别以OC,OA所在的直线为x轴,y轴建立平面直角坐标系,抛物线y=ax2+bx+c经过O,D,C三点.
如图,在矩形OABC中,AO=10,AB=8,沿直线CD折叠矩形OABC的一边BC,使点B落在OA边上的点E处,分别以OC,OA所在的直线为x轴,y轴建立平面直角坐标系,抛物线y=ax2+bx+c经过O,D,C三点.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
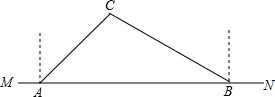 如图,要在后羿公园内的东西方向的两地之间修一条游客步行道路MN,已知C点周围50米范围内为中共华工委纪念馆,在MN上的点A处测得C在A的北偏东45°方向上,从A向东走150米到达B处,测得C在点B的北偏西60°方向上.
如图,要在后羿公园内的东西方向的两地之间修一条游客步行道路MN,已知C点周围50米范围内为中共华工委纪念馆,在MN上的点A处测得C在A的北偏东45°方向上,从A向东走150米到达B处,测得C在点B的北偏西60°方向上.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 2.2(1+2x)2=5 | B. | 2.2(1+2x)3=5 | ||
| C. | 2.2(1+x)+2.2(1+x2)=5 | D. | 2.2(1+x)+2.2(1+x)3=5 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
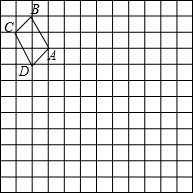 如图,在边长为1个单位长度的小正方形组成的网格中,给出了格点四边形ABCD(顶点是网格线的交点),按要求画出四边形AB1C1D1和四边形AB2C2D2.
如图,在边长为1个单位长度的小正方形组成的网格中,给出了格点四边形ABCD(顶点是网格线的交点),按要求画出四边形AB1C1D1和四边形AB2C2D2.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 1,$\sqrt{2}$,$\sqrt{3}$ | B. | $\sqrt{3}$,$\sqrt{4}$,$\sqrt{5}$ | C. | 5,6,7 | D. | 7,8,9 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com