
 小华同学学习了第二十五章《锐角三角比》后,对求三角形的面积方法进行了研究,得到了新的结论:
小华同学学习了第二十五章《锐角三角比》后,对求三角形的面积方法进行了研究,得到了新的结论: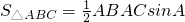 ;
;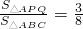 ?
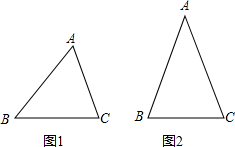
? 解:(1)如图1,
解:(1)如图1,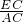 ,
, EC×AB=
EC×AB= AB×ACsinA;
AB×ACsinA; AQ×PE=
AQ×PE= ×(12-t)×APsinA=
×(12-t)×APsinA= ×(12-t)×2t×sinA=t(12-t)sinA,
×(12-t)×2t×sinA=t(12-t)sinA, BF×AC=
BF×AC= ×12×12sinA=72sinA,
×12×12sinA=72sinA,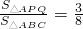 ,
,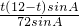 =
= ,
,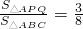 .
.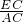 ,进而得出EC的长,即可得出答案;
,进而得出EC的长,即可得出答案;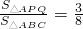 求出t的值即可.
求出t的值即可.

 字词句篇与同步作文达标系列答案
字词句篇与同步作文达标系列答案 走进文言文系列答案
走进文言文系列答案湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com