
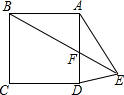
 如图,E为正方形ABCD外的一点,AE=AD,BE交AD于F,∠ADE=75°,则∠AFB的度数是60°.
如图,E为正方形ABCD外的一点,AE=AD,BE交AD于F,∠ADE=75°,则∠AFB的度数是60°. 分析 根据等腰三角形的性质得:∠AED=∠ADE=75°,由三角形内角和求出顶角∠DAE=30°,因为正方形ABCD可知:AB=AD及∠BAD=90°,则△ABE也是等腰三角形,求出∠ABE的度数,再由直角三角形的两个锐角互余求出结论.
解答 解:∵AD=AE,
∴∠AED=∠ADE=75°,
∴∠DAE=180°-75°-75°=30°,
∵四边形ABCD为正方形,
∴∠BAD=90°,AB=AD,
∴AB=AE,
∴∠ABE=∠AEB,
∵∠BAE=90°+30°=120°,
∴∠ABE=$\frac{180°-120°}{2}$=30°,
∴∠AFB=90°-30°=60°,
故答案为:60°.
点评 本题考查了正方形的性质,正方形的四个角都是直角,且各边都相等;在几何证明中常运用等边对等角和等角对等边来证明边相等或角相等;在三角形中,要熟练掌握三角形的内角和定理和直角三角形的两个锐角互余.


 学期复习一本通学习总动员期末加暑假延边人民出版社系列答案
学期复习一本通学习总动员期末加暑假延边人民出版社系列答案 芒果教辅暑假天地重庆出版社系列答案
芒果教辅暑假天地重庆出版社系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com