
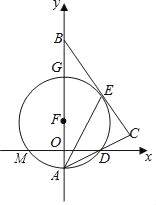
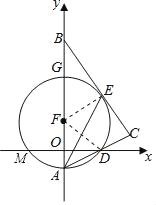
【题目】如图,在平面直角坐标系中,Rt△ABC的斜边AB在y轴上,边AC与x轴交于点D,经过A,D两点的圆的圆心F恰好在y轴上,⊙F与边BC相切于点E,与x轴交于点M,与y轴相交于另一点G,连接AE.
(1)求证:AE平分∠BAC;
(2)若点A,D的坐标分别为(0,﹣1),(2,0),求⊙F的半径;
(3)求经过三点M,F,D的抛物线的解析式.
【答案】(1)详见解析;(2)⊙F的半径为![]() ;(3)y=﹣
;(3)y=﹣![]() x2+
x2+![]() .
.
【解析】
(1)连接FE,先根据切线的性质知∠FEC=90°,结合∠C=90°证FE∥AC得∠EAC=∠FEA,根据FA=FE知∠FAE=∠FEA,从而得∠FAE=∠CAE,即可得证;
(2)连接FD,设⊙F的半径为r,根据FD2=(AF﹣AO)2+OD2知r2=(r﹣1)2+22,解之可得;
(3)根据圆的对称性得出点M的坐标,设抛物线的交点式,将点F坐标代入计算可得.
(1)连接FE,
∵⊙F与边BC相切于点E,
∴∠FEC=90°,
∵∠ACB=90°,
∴∠FEC+∠ACB=180°,
∴FE∥AC,
∴∠EAC=∠FEA,
∵FA=FE,
∴∠FAE=∠FEA,
∴∠FAE=∠CAE,
∴AE平分∠BAC;
(2)连接FD,
设⊙F的半径为r,
∵A(0,﹣1),D(2,0),
∴OA=1,OD=2,
在Rt△FOD中,FD2=(AF﹣AO)2+OD2,
∴r2=(r﹣1)2+22,
解得:r=![]() ,
,
∴⊙F的半径为![]() ;
;
(3)∵FA=r=![]() ,OA=1,FO=
,OA=1,FO=![]() ,
,
∴F(0,![]() ),
),
∵直径AG垂直平分弦MD,点M和点D(2,0)关于y轴对称轴,
∴M(﹣2,0),
设抛物线解析式为y=a(x+2)(x﹣2),
将点F(0,![]() )代入,得:﹣4a=
)代入,得:﹣4a=![]() ,
,
解得:a=﹣![]() ,
,
则抛物线解析式为y=﹣![]() (x+2)(x﹣2)=﹣
(x+2)(x﹣2)=﹣![]() x2+
x2+![]() .
.


科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,点E,F分别在边AB,BC上,且AE=![]() AB,将矩形沿直线EF折叠,点B恰好落在AD边上的点P处,连接BP交EF于点Q,对于下列结论:①EF=2BE;②PF=2PE;③FQ=4EQ;④△PBF是等边三角形.其中正确的是( )
AB,将矩形沿直线EF折叠,点B恰好落在AD边上的点P处,连接BP交EF于点Q,对于下列结论:①EF=2BE;②PF=2PE;③FQ=4EQ;④△PBF是等边三角形.其中正确的是( )

A. ①② B. ②③ C. ①③ D. ①④
查看答案和解析>>
科目:初中数学 来源: 题型:
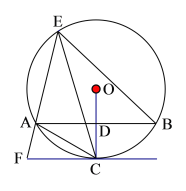
【题目】如图,在⊙O中,半径OC⊥弦AB于点D,点E为优弧AB上一点,连接AE、BE、AC,过点C的直线与EA延长线交于点F,且∠ACF=![]() ∠AEB.
∠AEB.
(1)求证:CF与⊙O相切;
(2)若∠AEB=60°,AB=4![]() ,求⊙O的半径;
,求⊙O的半径;
(3)在(2)的条件下,若AE=4![]() ,求EC的长.
,求EC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法不正确的是( )
A. 设![]() 为单位向量,那么
为单位向量,那么![]()
B. 已知![]() 、
、![]() 、
、![]() 都是非零向量,如果
都是非零向量,如果![]() ,
,![]() ,那么
,那么![]()
C. 四边形![]() 中,如果满足
中,如果满足![]() ,
,![]() ,那么这个四边形一定是平行四边形
,那么这个四边形一定是平行四边形
D. 平面内任意一个非零向量都可以在给定的两个不平行向量的方向上分解
查看答案和解析>>
科目:初中数学 来源: 题型:
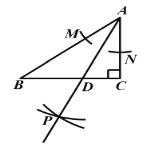
【题目】如图,在![]() 中,
中,![]() ,
,![]() ,
,![]() ,以点
,以点![]() 为圆心,以任意长为半径作弧,分别交
为圆心,以任意长为半径作弧,分别交![]() 于点M,N,再分别以M,N为圆心,以大于
于点M,N,再分别以M,N为圆心,以大于![]() 的长为半径作弧,两弧交于点
的长为半径作弧,两弧交于点![]() ,作射线
,作射线![]() 交
交![]() 于点
于点![]() ,则
,则![]() 的长是__________.
的长是__________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,排球运动员站在点O处练习发球,将球从O点正上方2m的A处发出,把球看成点,其运行的高度y(m)与运行的水平距离x(m)满足关系式y=a(x![]() k)2+h.已知球与O点的水平距离为6m时,达到最高2.6m,球网与O点的水平距离为9m.高度为2.43m,球场的边界距O点的水平距离为18m,则下列判断正确的是( )
k)2+h.已知球与O点的水平距离为6m时,达到最高2.6m,球网与O点的水平距离为9m.高度为2.43m,球场的边界距O点的水平距离为18m,则下列判断正确的是( )
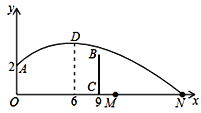
A. 球不会过网 B. 球会过球网但不会出界
C. 球会过球网并会出界 D. 无法确定
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,经过正方形ABCD的顶点A在其外侧作直线AP,点B关于直线AP的对称点为E,连接BE、DE,其中DE交直线AP于点F.
(1)依题意补全图1.
(2)若∠PAB=30°,求∠ADF的度数.
(3)如图,若45°<∠PAB<90°,用等式表示线段AB,FE,FD之间的数量关系,并证明.

查看答案和解析>>
科目:初中数学 来源: 题型:
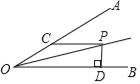
【题目】如图,已知∠AOB=30°,P是∠AOB平分线上一点,CP∥OB,交OA于点C,PD⊥OB,垂足为点D,且PC=8,则PD的长为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
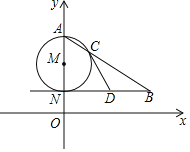
【题目】如图,AN是⊙M的直径,NB∥x轴,AB交⊙M于点C.
(1)若点A(0,6),N(0,2),∠ABN=30°,求点B的坐标;
(2)若D为线段NB的中点,求证:直线CD是⊙M的切线.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com