
 阳光课堂课时优化作业系列答案
阳光课堂课时优化作业系列答案科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
| 1 | 2 |
查看答案和解析>>
科目:初中数学 来源: 题型:
 正确?若正确,请说明理由;若不正确,请举出一个反例说明.
正确?若正确,请说明理由;若不正确,请举出一个反例说明.查看答案和解析>>
科目:初中数学 来源: 题型:
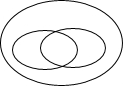
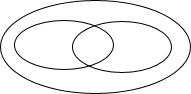
(2011广西崇左,22,10分)(本小题满分10分)矩形、菱形、正方形都是平行四边形,但它们都是有特殊条件的平行四边形,正方形不仅是特殊的矩形,也是特殊的菱形.因此,我们可利用矩形、菱形的性质来研究正方形的有关问题.回答下列问题:
(1)将平行四边形、矩形、菱形、正方形填入它们的包含关系的下图中.
(2)要证明一个四边形是正方形,可先证明四边形是矩形,再证明这个矩形的_______相等;或者先证明四边形是菱形,在证明这个菱形有一个角是________ .
(3)某同学根据菱形面积计算公式推导出对角线长为a的正方形面积是S=0.5a2,对此结论,你认为是否正确?若正确,请说明理由;若不正确,请举出一个反例说明.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com