
分析 (1)根据二次项系数非零结合根的判别式△>0,即可得出关于m的一元一次不等式组,解之即可得出实数m的取值范围;
(2)根据根的判别式△>0结合常数项小于0,即可得出关于a的一元一次不等式组,解之即可得出实数a的取值范围.
解答 解:(1)∵关于x的方程mx2+(2m+1)x+m=0有两个不相等的实数根,
∴$\left\{\begin{array}{l}{m≠0}\\{△=(2m+1)^{2}-4{m}^{2}>0}\end{array}\right.$,
解得:m>-$\frac{1}{4}$且m≠0.
(2)∵关于x的一元二次方程x2-x+a-4=0的一根大于零,另一根小于零,
∴$\left\{\begin{array}{l}{△=(-1)^{2}-4(a-4)>0}\\{{x}_{1}+{x}_{2}=a-4<0}\end{array}\right.$,
解得:a<4.
点评 本题考查了根与系数的关系、根的判别式以及一元二次方程的定义,解题的关键是:(1)根据二次项系数非零结合根的判别式△>0,列出关于m的一元一次不等式组;(2)根据根的判别式△>0结合常数项小于0,列出关于a的一元一次不等式组.


科目:初中数学 来源: 题型:解答题
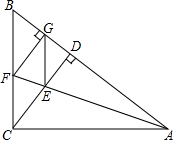 如图,在Rt△ABC中,∠ACB=90°,CD为AB边上的高,∠CAB的平分线交CD于点E,交CB于点F,过点F作FG⊥AB于点G,连接GE.求证:四边形CEGF是菱形.
如图,在Rt△ABC中,∠ACB=90°,CD为AB边上的高,∠CAB的平分线交CD于点E,交CB于点F,过点F作FG⊥AB于点G,连接GE.求证:四边形CEGF是菱形.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
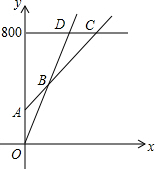 某市游泳馆为了满足不同顾客的需求,设计了三种游泳票:普通票价每次20元/张;金卡售价800元/张,每次凭卡不再收费;银卡售价200元/张,每次凭卡另收10元.这样顾客可根据游泳次数的多少选择不同的消费方式.普通票全年正常出售,两种优惠卡仅限暑期使用,不限次数.设游泳x次时,所需总费用为y元.
某市游泳馆为了满足不同顾客的需求,设计了三种游泳票:普通票价每次20元/张;金卡售价800元/张,每次凭卡不再收费;银卡售价200元/张,每次凭卡另收10元.这样顾客可根据游泳次数的多少选择不同的消费方式.普通票全年正常出售,两种优惠卡仅限暑期使用,不限次数.设游泳x次时,所需总费用为y元.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
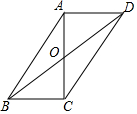 如图,在?ABCD中,对角线AC,BD交于点O,AC⊥BC,若$\frac{BD}{CD}$=$\frac{8}{5}$,则$\frac{BC}{AC}$=$\frac{\sqrt{39}}{6}$.
如图,在?ABCD中,对角线AC,BD交于点O,AC⊥BC,若$\frac{BD}{CD}$=$\frac{8}{5}$,则$\frac{BC}{AC}$=$\frac{\sqrt{39}}{6}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com