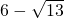练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    若a、b分别是数学公式的整数部分和小数部分．求代数式8ab-b2的值．

    解：∵＜＜，
    ∴的整数部分在3和4之间，
    ∴6-的整数部分a=2，b=4-，
    则8ab-b2=8×2×（4-）-（4-）2
    =64-16-（16-8+13）
    =35-8．
    分析：首先判断出的整数部分在3和4之间，即6-的整数部分a=2，则b=4-，然后把a和b的值代入代数式求值即可．
    点评：本题主要考查了代数式求值，涉及到比较有理数和无理数的大小，解题的关键在于用正确的形式表示出6-的整数部分和小数部分，然后代入求值即可．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：022

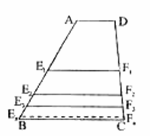
    如图，在梯形ABCD中，AD∥BC，AD=a，BC=b.若E1、F1分别是AB、DC的中点，则；若分别是的中点，则；当分别是的中点，则；若分别是的中点，根据上述规律猜想EnFn=____(n≥1，n为整数).

    查看答案和解析>>

    科目：初中数学 来源：2012年苏教版初中数学八年级上2.3平方根练习卷（解析版） 题型：选择题

    若x、y分别是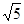的整数部分与小数部分，则2xy+y2的值为      (    )

    A.  2       B.5        C.8         D. 1

     

    查看答案和解析>>

    科目：初中数学 来源：2009-2010学年四川省自贡市沿滩区仙市中学九年级（上）第一学月数学试卷（解析版） 题型：解答题

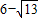    若a、b分别是的整数部分和小数部分．求代数式8ab-b2的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：阅读理解

    阅读以下材料：

    若关于的三次方程（、、为整数）有整数解，则将代入方程得：    

         ∴

     ∵、、都是整数    ∴是整数    ∴是的因数．

    上述过程说明：整数系数方程的整数解只能是常数项的因数．如：∵方程中常数项－2的因数为：±1和±2，∴将±1和±2分别代入方程得：=－2是该方程的整数解，－1、1、2不是方程的整数解．

    解决下列问题：

    （1）根据上面的学习，方程的整数解可能          ；

    （2）方程有整数解吗？若有，求出整数解；若没有，说明理由．

    查看答案和解析>>

    同步练习册答案