
【题目】如图,已知在△ABC中,∠1=∠2.
(1)请你添加一个与直线AC有关的条件,由此可得出BE是△ABC的外角平分线;
(2)请你添加一个与∠1有关的条件,由此可得出BE是△ABC的外角平分线;
(3)如果“已知在△ABC中,∠1=∠2不变”,请你把(1)中添加的条件与所得结论互换,所得的命题是否是真命题,理由是什么?

 小学能力测试卷系列答案
小学能力测试卷系列答案科目:初中数学 来源: 题型:
【题目】下列式子错误的是( )
A.cos40°=sin50°
B.tan15°tan75°=1
C.sin225°+cos225°=1
D.sin60°=2sin30°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下表是某水站记录的潮汛期某河一周内的水位变化情况(正号表示水位比前一天上升,负号表示水位比前一天下降,上周的水位恰好达到警戒水位,单位:米)
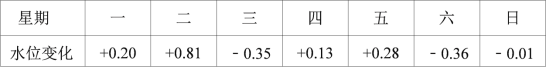
(1)本周哪一天河流的水位最高,哪一天河流的水位最低,它们位于警戒水位之上还是之下,与警戒水位的距离分别是多少?
(2)与上周末相比,本周末河流的水位是上升还是下降了?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在四边形ABDC中,AC=AB,DC=DB,∠CAB=60°,∠CDB=120°,E是AC上一点,F是AB延长线上一点,且CE=BF.

(1)试说明:DE=DF;
(2)在图中,若G在AB上且∠EDG=60°,试猜想CE、EG、BG之间的数量关系并证明所归纳结论;
(3)若题中条件“∠CAB=60°,∠CDB=120°”改为∠CAB=α,∠CDB=180°-α,G在AB上,∠EDG满足什么条件时,(2)中结论仍然成立?(只写结果不要证明).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校团委组织了有奖征文活动,并设立了一、二、三等奖,根据设奖情况买了50 件奖品,其二等奖奖品的件数比一等奖奖品的件数的2 倍少10, 各种奖品的单价如下表所示:

如果计划一等奖奖品买x件,买5 件奖品的总数是y元.
(1)先填表,再用含x的代数式表示y并化简;
(2)若一等奖奖品买10件,则共花费多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知AB=AD,那么添加下列一个条件后,仍无法判定△ABC≌△ADC的是( )

A. CB=CD B. ∠BAC=∠DAC C. ∠BCA=∠DCA D. ∠B=∠D=90°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC和Rt△DCB中,AB=DC,∠A=∠D=90°,AC与BD交于点O,则有△________≌△________,其判定依据是________,还有△________≌△________,其判定依据是________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】按要求完成下列题目.
![]() 求:
求:![]() 的值.
的值.
对于这个问题,可能有的同学接触过,一般方法是考虑其中的一般项,注意到上面和式的每一项可以写成![]() 的形式,而
的形式,而![]() ,这样就把
,这样就把![]() 一项
一项![]() 分
分![]() 裂成了两项.
裂成了两项.
试着把上面和式的每一项都裂成两项,注意观察其中的规律,求出上面的和,并直接写出![]() 的值.
的值.
![]() 若
若![]()
![]() 求:A、B的值:
求:A、B的值:
![]() 求:
求:![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com