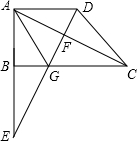
解:(1)证明:过点M作MG⊥AD交AD于G;
∵AM∥DC,∴∠AMB=∠C;
∵∠B=90°,AB=8,
∴

,
∴

,∴BM=6;
∵AD∥BC,AB∥MG,
∴AG=BM=6,
∵AD=12,∴AG=GD,
∴△AGM≌△DGM,
∴AM=DM.

(2)∵∠FEM=∠AMB,∠AMB=∠MAE,
∴∠MAE=∠MEF,
∵∠AME=∠EMF,
∴△AEM∽△EFM;
∴

,
∵

,
∴
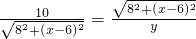
,
∴

;
定义域为:0<x<12.
(3)∵∠EFM=∠MAE+∠AEF>∠FEM,
∴EM≠FM,
∴若△EFM为等腰三角形,则EF=EM或EF=FM;
①当EF=FM时,
12-x=10,∴x=2;
②当EF=EM时,
∵∠FME=∠FEM=∠MAE,
∴AE=EM,
∴

,
∴

.
(4)若⊙M与⊙E外切,则

,
∴
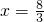
,
∴

;
若⊙M与⊙E内切,则

.
方程无解.
分析:(1)此题要通过构造全等三角形求解,过M作MG⊥AD于G,则AG=BM,在Rt△ABM中,由∠AMB(即∠C)的正切值可求得BM的长,也就得到了AG的长,此时发现G是AD的中点,即可证得△MAG≌△MDG,由此可得到所求的结论.
(2)由于AD∥BC,易得∠MAE=∠FEM=∠AMB,即可证得△AEM∽△EFM,分别表示出ME
2、MF、MA的长,根据相似三角形得到的比例线段即可得到y、x的函数关系式.
(3)根据三角形的外角性质知:∠EFM>∠FAE=∠FEM,因此EM≠FM,所以分两种情况讨论即可:
①EF=EM,此时∠EFM=∠EMF,由于∠EFM=∠AEF=∠FEM+∠AEF,由此可证得AE=MA=10,由此可得到DE的长;
②EF=FM,此时∠FEM=∠EMF=∠EAM,即AE=EM,可令两条线段的表达式相等,即可求得此时DE的长.
(4)此题要分两种情况讨论:
①两圆外切,那么EM=BM+DE,分别表示出各线段的长,根据上面的等量关系列方程求得x的值,即可得到DE的长,以DE为底、AB为高即可得△EMD的面积;
②两圆内切,方法同上.
点评:此题考查了全等三角形的判定和性质、直角梯形的性质、以及相似三角形、全等三角形的判定和性质,圆与圆的位置关系等知识,综合性强,难度较大.

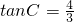 ,AM∥DC,E
,AM∥DC,E 、F分别是线段AD、AM上的动点(点E与A、D不重合)且∠FEM=∠AMB,设DE=x,MF=y.
、F分别是线段AD、AM上的动点(点E与A、D不重合)且∠FEM=∠AMB,设DE=x,MF=y. ,
, ,∴BM=6;
,∴BM=6;
 ,
, ,
,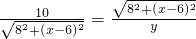 ,
, ;
; ,
, .
. ,
,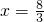 ,
, ;
; .
.

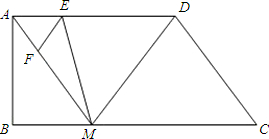 、F分别是线段AD、AM上的动点(点E与A、D不重合)且∠FEM=∠AMB,设DE=x,MF=y.
、F分别是线段AD、AM上的动点(点E与A、D不重合)且∠FEM=∠AMB,设DE=x,MF=y.