
分析 设x+y=A,x-y=B,方程变形后,利用代入消元法求出A与B的值,进而确定出x与y的值即可.
解答 解:设x+y=A,x-y=B,
方程组变形得:$\left\{\begin{array}{l}{\frac{A}{2}+\frac{B}{3}=6}\\{2A-3B=24}\end{array}\right.$,
整理得:$\left\{\begin{array}{l}{3A+2B=36①}\\{2A-3B=24②}\end{array}\right.$,
①×3+②×2得:13A=156,即A=12,
把A=12代入②得:B=0,
∴$\left\{\begin{array}{l}{x+y=12}\\{x-y=0}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{x=6}\\{y=6}\end{array}\right.$.
点评 此题考查了解二元一次方程组,利用了消元的思想,消元的方法有:代入消元法与加减消元法.


 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 2.33×105 | B. | 2.33×106 | C. | 2.33×107 | D. | 2.33×108 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 6.75×104吨 | B. | 67.5×103吨 | C. | 0.675×103吨 | D. | 6.75×10-4吨 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 设上坡路长x千米,可列方程$\frac{x}{3}-\frac{x}{5}=\frac{54}{60}-\frac{42}{60}$ | |
| B. | 设上坡路长x千米,平路长y千米,可列方程组$\left\{\begin{array}{l}\frac{x}{3}+\frac{y}{4}=\frac{54}{60}\\ \frac{x}{5}+\frac{y}{4}=\frac{42}{60}.\end{array}\right.$ | |
| C. | 列算式(54-42)÷(5-3)即可求出上坡路长. | |
| D. | 根据条件,能求出甲地到乙地的全程是3.1千米. |
查看答案和解析>>
科目:初中数学 来源:2016-2017学年四川省成都市金堂县八年级上学期期末考试数学试卷就(解析版) 题型:判断题
已知 中,
中,  .点
.点 从点
从点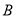 出发沿线段
出发沿线段 移动,同时点
移动,同时点 从点
从点 出发沿线段
出发沿线段 的延长线移动,点
的延长线移动,点 、
、 移动的速度相同,
移动的速度相同,  与直线
与直线 相交于点
相交于点 .
.
(1)如图①,当点 为
为 的中点时,求
的中点时,求 的长;
的长;
(2)如图②,过点 作直线
作直线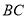 的垂线,垂足为
的垂线,垂足为 ,当点
,当点 、
、 在移动的过程中,设
在移动的过程中,设 ,
,  是否为常数?若是请求出
是否为常数?若是请求出 的值,若不是请说明理由.
的值,若不是请说明理由.
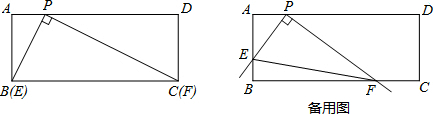
(3)如图③,E为BC的中点,直线CH垂直于直线AD,垂足为点H,交AE的延长线于点M;直线BF垂直于直线AD,垂足为F;找出图中与BD相等的线段,并证明.



查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在△ABC中,AB=7,BC=4$\sqrt{2}$,∠B=45°,动点P、Q同时出发,点P沿A-C-B运动,在边AC的速度为每秒1个单位长度,在边CB的速度为每秒$\sqrt{2}$个单位长度;点Q沿B-A-B以每秒2个单位长度的速度运动,其中一个动点到达终点时,另一个动点也停止运动,在运动过程中,过点P作AB的垂线与AB交于点D,以PD为边向由作正方形PDEF;过点Q作AB的垂线l.设正方形PDEF与△ABC重叠部分图形的面积为y(平方单位),运动时间为t(秒).
如图,在△ABC中,AB=7,BC=4$\sqrt{2}$,∠B=45°,动点P、Q同时出发,点P沿A-C-B运动,在边AC的速度为每秒1个单位长度,在边CB的速度为每秒$\sqrt{2}$个单位长度;点Q沿B-A-B以每秒2个单位长度的速度运动,其中一个动点到达终点时,另一个动点也停止运动,在运动过程中,过点P作AB的垂线与AB交于点D,以PD为边向由作正方形PDEF;过点Q作AB的垂线l.设正方形PDEF与△ABC重叠部分图形的面积为y(平方单位),运动时间为t(秒).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com