
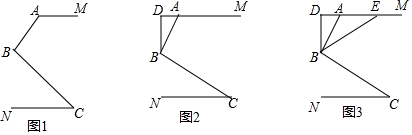
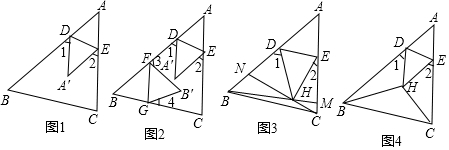
分析 (1)过点B作BE∥AM,则AM∥BE∥NC,再由平行线的性质即可得出结论;
(2)过点B作BF∥DM,则∠ADB+∠DBF=180°,再由BD⊥AM,AB⊥BC可得出∠ABD=∠CBF,再由平行线的性质即可得出结论;
(3)设∠DEB=x°,由(2)可得∠ABD=∠C,由∠C=∠DEB可得出∠ABD=∠C=∠DEB=x°,过点B作BF∥DM,根据平行线的性质可得出∠DBC=∠ABC+∠ABD=90°+x°.再由BE平分∠DBC可知∠DBC=2∠CBE=4x°,据此可得出x的值.
解答 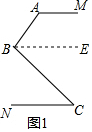 (1)解:过点B作BE∥AM,则AM∥BE∥NC,
(1)解:过点B作BE∥AM,则AM∥BE∥NC,
∵BE∥NC,∠C=40°,
∴∠CBE=∠C=40°.
∵AB⊥BC,
∴∠ABC=90°,
∴∠ABE=90°-40°=50°.
∵AM∥BE,
∴∠BAM+∠ABE=18°,
∴∠BAM=180°-50°=130°.
故答案为:130°;
(2)证明:如图2,过点B作BF∥DM,则∠ADB+∠DBF=180°.
∵BD⊥AM,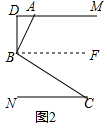
∴∠ADB=90°.
∴∠DBF=90°,∠ABD+∠ABF=90°.
又∵AB⊥BC,
∴∠CBF+∠ABF=90°.
∴∠ABD=∠CBF.
∵AM∥CN,
∴BF∥CN,
∴∠C=∠CBF.
∴∠ABD=∠C.
(3)解:设∠DEB=x°,由(2)可得∠ABD=∠C,
∵∠C=∠DEB,
∴∠ABD=∠C=∠DEB=x°.
过点B作BF∥DM,如图3,
∴∠DEB=∠EBF,∠C=∠FBC.
∴∠CBE=∠EBF+∠FBC=∠DEB+∠C=2x°.
∵∠DBC=∠ABC+∠ABD=90°+x°.
∵BE平分∠DBC,
∴∠DBC=2∠CBE=4x°,即4x=90+x,解得x=30.
∴∠DEB的度数为30°.
点评 本题考查的是平行线的性质,根据题意作出辅助线,构造出平行线,利用平行线的性质求解是解答此题的关键.


科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 3x2•4x2=12x2 | B. | $\frac{x^2}{y^2}=\frac{x}{y}$(y≠0) | ||
| C. | 2$\sqrt{x}+3\sqrt{y}=5\sqrt{xy}$(x≥0,y≥0) | D. | xy2÷$\frac{1}{2y}=2x{y^3}$(y≠0) |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
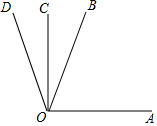 ∠AOC为直角,OC是∠BOD的平分线,且∠AOB=57.65°,则∠AOD的度数是( )
∠AOC为直角,OC是∠BOD的平分线,且∠AOB=57.65°,则∠AOD的度数是( )| A. | 122°20′ | B. | 122°21′ | C. | 122°22′ | D. | 122°23′ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com