
【题目】在平面直角坐标系![]() 中,抛物线
中,抛物线![]() .
.
![]() 当抛物线的顶点在
当抛物线的顶点在![]() 轴上时,求该抛物线的解析式;
轴上时,求该抛物线的解析式;
![]() 不论
不论![]() 取何值时,抛物线的顶点始终在一条直线上,求该直线的解析式;
取何值时,抛物线的顶点始终在一条直线上,求该直线的解析式;
![]() 若有两点
若有两点![]() ,且该抛物线与线段
,且该抛物线与线段![]() 始终有交点,请直接写出
始终有交点,请直接写出![]() 的取值范围.
的取值范围.
【答案】(1)![]() ;(2)抛物线的顶点在直线
;(2)抛物线的顶点在直线![]() 上;(3)
上;(3)![]() .
.
【解析】
(1)利用配方法求出抛物线的顶点坐标是(m,﹣m+1),根据顶点在x轴上,得出﹣m+1=0,求出m=1,即可得出抛物线的解析式;
(2)由于抛物线的顶点坐标是(m,﹣m+1),即可得出顶点在直线y=﹣x+1上;
(3)把点A(﹣1,0)代入y=﹣x2+2mx﹣m2﹣m+1,求出m的值,再把B(1,0)代入y=﹣x2+2mx﹣m2﹣m+1,求出m的值,即可求解.
(1)∵y=﹣x2+2mx﹣m2﹣m+1=﹣(x﹣m)2﹣m+1,∴顶点坐标是(m,﹣m+1).
∵抛物线的顶点在x轴上,∴﹣m+1=0,∴m=1,∴y=﹣x2+2x﹣1;
(2)∵抛物线y=﹣x2+2mx﹣m2﹣m+1的顶点坐标是(m,﹣m+1),∴抛物线的顶点在直线y=﹣x+1上;
(3)当抛物线y=﹣x2+2mx﹣m2﹣m+1过点A(﹣1,0)时,﹣1﹣2m﹣m2﹣m+1=0,解得m1=0,m2=﹣3,当抛物线y=﹣x2+2mx﹣m2﹣m+1过点B(1,0)时,﹣1+2m﹣m2﹣m+1=0,解得m1=0,m2=1,故﹣3≤m≤1.


 优百分课时互动系列答案
优百分课时互动系列答案 开心蛙状元作业系列答案
开心蛙状元作业系列答案科目:初中数学 来源: 题型:
【题目】已知等腰△ABC中,AB=AC,∠ABC的平分线交AC于D,过点A作AE // BC交BD的延长线于点E,∠CAE的平分线交BE于点F.
(1)①如图,若∠BAC=36o,求证:BD=EF;
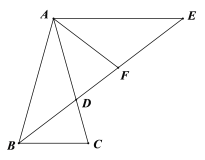
②如图,若∠BAC=60o,求![]() 的值;
的值;
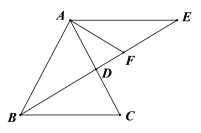
(2)如图,若∠BAC=60o,过点D作DG// BC,交AB于点G,点N为BC中点,点P, M分别是GD, BG上的动点,且∠PNM=60°. 求证:AP=PN=MN.
查看答案和解析>>
科目:初中数学 来源: 题型:
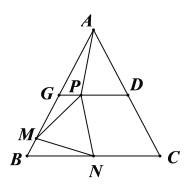
【题目】如图,△ABC中,BA=BC,CO⊥AB于点O,AO=4,BO=6.
(1)求BC,AC的长;
(2)若点D是射线OB上的一个动点,作DE⊥AC于点E,连结OE.
①当点D在线段OB上时,若△AOE是以AO为腰的等腰三角形,请求出所有符合条件的OD的长.
②设DE交直线BC于点F,连结OF,CD,若S△OBF:S△OCF=1:4,则CD的长为 (直接写出结果).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,点A(2,4),B(4,2),在x轴上取一点P,使点P到点A和点B的距离之和最小,则点P的坐标是_________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场一品牌服装,销售一件可获利![]() 元,为在十一期间增加盈利,进行促销活动,决定采取降价措施.根据以往销售经验及市场调查发现,每件服装降价
元,为在十一期间增加盈利,进行促销活动,决定采取降价措施.根据以往销售经验及市场调查发现,每件服装降价![]() (元)与每天的销售量
(元)与每天的销售量![]() (件)之间的关系如下表
(件)之间的关系如下表
|
|
|
|
|
| … |
|
|
|
|
|
| … |
![]() 请你按照上表,求
请你按照上表,求![]() 与
与![]() 之间的函数解析式.
之间的函数解析式.
![]() 为保证每天能盈利
为保证每天能盈利![]() 元,又能吸引顾客,每件服装应降价多少元?
元,又能吸引顾客,每件服装应降价多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某宾馆有客房![]() 间供游客居住,当每间客房的定价为每天
间供游客居住,当每间客房的定价为每天![]() 元时,客房恰好全部住满;如果每间客房每天的定价每增加
元时,客房恰好全部住满;如果每间客房每天的定价每增加![]() 元,就会减少
元,就会减少![]() 间客房出租.设每间客房每天的定价增加
间客房出租.设每间客房每天的定价增加![]() 元,宾馆出租的客房为
元,宾馆出租的客房为![]() 间.求:
间.求:
![]() 关于
关于![]() 的函数关系式;
的函数关系式;
![]() 如果某天宾馆客房收入
如果某天宾馆客房收入![]() 元,那么这天每间客房的价格是多少元?
元,那么这天每间客房的价格是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,在长方形ABCD中,AB=4,AD=6.延长BC到点E,使CE=2,连接DE,动点P从点B出发,以每秒2个单位的速度沿BC﹣CD﹣DA向终点A运动,设点P的运动时间为t秒,当t的值为( )秒时,△ABP和△DCE全等.

A. 1 B. 1或3 C. 1或7 D. 3或7
查看答案和解析>>
科目:初中数学 来源: 题型:
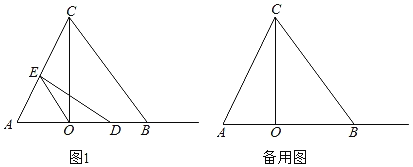
【题目】(1)阅读理解:
我们知道,只用直尺和圆规不能解决的三个经典的希腊问题之一是三等分任意角,但是这个任务可以借助如图1所示的一边上有刻度的勾尺完成,勾尺的直角顶点为P,
“宽臂”的宽度=PQ=QR=RS,(这个条件很重要哦!)勾尺的一边MN满足M,N,Q三点共线(所以PQ⊥MN).
下面以三等分∠ABC为例说明利用勾尺三等分锐角的过程:
第一步:画直线DE使DE∥BC,且这两条平行线的距离等于PQ;
第二步:移动勾尺到合适位置,使其顶点P落在DE上,使勾尺的MN边经过点B,同时让点R落在∠ABC的BA边上;
第三步:标记此时点Q和点P所在位置,作射线BQ和射线BP.
请完成第三步操作,图中∠ABC的三等分线是射线 、 .
(2)在(1)的条件下补全三等分∠ABC的主要证明过程:
∵ ,BQ⊥PR,
∴BP=BR.(线段垂直平分线上的点与这条线段两个端点的距离相等)
∴∠ =∠ .
∵PQ⊥MN,PT⊥BC,PT=PQ,
∴∠ =∠ .
(角的内部到角的两边距离相等的点在角的平分线上)
∴∠ =∠ =∠ .
(3)在(1)的条件下探究:![]() 是否成立?如果成立,请说明理由;如果不成立,请在图2中∠ABC的外部画出
是否成立?如果成立,请说明理由;如果不成立,请在图2中∠ABC的外部画出![]() (无需写画法,保留画图痕迹即可).
(无需写画法,保留画图痕迹即可).

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com