Question

10．在平面直角坐标系中，点O为原点，点A的坐标为（0，3），以点A为圆心，OA为半径在y轴右侧作半圆A，直线l：y=x+m交x轴于点C．
（1）如图1，当m=0时，直线l与半圆A分别相交于点O，D，求此时OD的长；
（2）当m=-3时，在半圆A上取一点P，过点P作PH⊥l于点H．
①如图2，当直线PH与半圆A相切时，求此时点P的坐标；
②如图3，设点P的坐标为（a，b），过点P作PE⊥y于点E，连接EH，△PEH的其中两边之比能否为$\sqrt{2}$：1？若能，求此时a与b的关系；若不能，请说明理由．

Answer 1

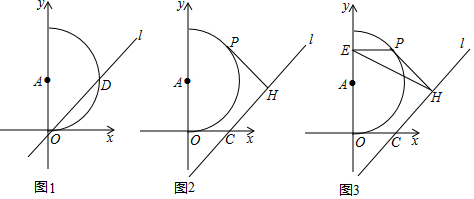
分析 （1）由直线y=x+m可知，∠AOD=45°，所以△AOD是等腰直角三角形，所以OD=$\sqrt{2}$OA；
（2）①连接AP并延长交于x轴于点B，过点P作PF⊥x轴于点F，由PH是⊙A的切线可知PB∥l，再由（1）可知：△PBF是等腰三角形，从而求出PF与BF的长度．
②根据点P的坐标分别求出PE，PH，EH的长度，由于△PEH的其中两边之比为$\sqrt{2}$：1，共分6种情况进行讨论，分别求出a与b的值即可．

解答 解：（1）当m=0时，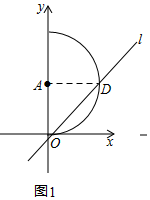
此时直线l为：y=x，
∴∠AOD=45°，
连接AD，
∴OA=AD，
∴△AOD是等腰直角三角形，
∴OD=$\sqrt{2}$OA=3$\sqrt{2}$；
（2）①连接AP并延长交于x轴于点B，过点P作PF⊥x轴于点F，
∵PH是⊙A的切线，
∴∠APH=∠PHC=90°，
∴AP∥l，
由（1）可知：∠PBF=45°，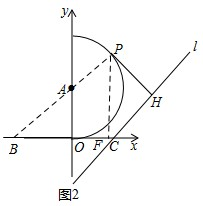
∵OA=3，
∴AB=$\sqrt{2}$OA=3$\sqrt{2}$，
∴BP=AB+AP=3$\sqrt{2}$+3，
∵BP=$\sqrt{2}$PF，
∴PF=3+$\frac{3\sqrt{2}}{2}$，
∴OF=BF-OB=PF-OB=$\frac{3\sqrt{2}}{2}$，
∴P的坐标为（$\frac{3\sqrt{2}}{2}$，3+$\frac{3\sqrt{2}}{2}$），
②连接AP，过点P作PF⊥x轴于点F，且交于l于点G，
过点H作HN⊥y轴于点N，交PF于点M，
∵P（a，b），且0≤a≤3，0≤b≤6，
∴PE=MN=OF=a，PF=b，
令y=0代入y=x-3，
∴C（3，0）
∴OC=3，
∴CF=3-a，
∵∠OCG=45°，
∴∠PHM=∠FGC=45°，
∴FG=CF=3-a，
∴PG=PF+FG=3-a+b，
∴PH=$\frac{PG}{\sqrt{2}}$=$\frac{3-a+b}{\sqrt{2}}$，
∴PM=$\frac{PH}{\sqrt{2}}$=$\frac{3-a+b}{2}$，
∴MH=EN=PM=$\frac{3-a+b}{2}$，
∴NH=MH+MN=$\frac{a+b+3}{2}$，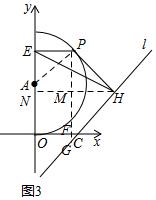
∴在Rt△EHN中，
由勾股定理可知：EH²=（$\frac{a+b+3}{2}$）²+（$\frac{3-a+b}{2}$）²，
∴EH²=$\frac{{a}^{2}+{b}^{2}+6b+9}{2}$，
在Rt△APE中，
由勾股定理可知：a²+（b-3）²=9，
当PE=$\sqrt{2}$PH时，
∴a=3-a+b，
∴b=2a-3，
当PH=$\sqrt{2}$PE时，
∴2a=3-a+b，
∴b=3a-3，
当PE=$\sqrt{2}$EH时，
∴PE²=2EH²，
∴a²=a²+b²+6b+9，
∴b²+6b+9=0，
∴b=-3，不符合题意，
当EH=$\sqrt{2}$PE时，
∴$\frac{{a}^{2}+{b}^{2}+6b+9}{2}$=2a²，
化简可得：b²+6b+9=3a²，
∴（b+3）²=3a²，
∵0≤a≤3，0≤b≤6，
∴b+3=$\sqrt{3}$a，
当EH=$\sqrt{2}$PH时，
∴EH²=2PH²，
∴（$\frac{a+b+3}{2}$）²+（$\frac{3-a+b}{2}$）²=2×$\frac{（3-a+b）^{2}}{2}$，
化简可得：（a+b+3）²=3（3-a+b）²，
∵∵0≤a≤3，0≤b≤6，
∴a+b+3=$\sqrt{3}$（3-a+b），
化简整理可得：（$\sqrt{3}$+1）a+（1-$\sqrt{3}$）b+3（1-$\sqrt{3}$）=0，
当PH=$\sqrt{2}$EH，
∴PH²=2EH²，
∴$\frac{（3-a+b）^{2}}{2}$=2×[（$\frac{a+b+3}{2}$）²+（$\frac{3-a+b}{2}$）²]
∴化简整理可得：（a+b+3）²=0，
∴a+b+3=0，
∵0≤a≤3，0≤b≤6，
∴a+b+3=0无解，此情况不符合题意．
综上所述，△PEH的其中两边之比为$\sqrt{2}$：1时，a与b的关系为：b=2a-3或b=3a-3或b+3=$\sqrt{3}$a或（$\sqrt{3}$+1）a+（1-$\sqrt{3}$）b+3（1-$\sqrt{3}$）=0，

点评 本题考查圆的综合问题，涉及等腰直角三角形的性质，一元二次方程的解法，切线的性质，平行线的性质等知识，综合程度较高．