
【题目】在平面直角坐标系xOy中,对于点P(x,y),我们把点![]() (-y+1,x+1)叫做点P伴随点.已知点A1的伴随点为A2,点A2的伴随点为A3,点A3的伴随点为A4,…,这样依次得到点A1,A2,A3,…,An,….若点A1的坐标为(2,4),点A2017的坐标为 ( )
(-y+1,x+1)叫做点P伴随点.已知点A1的伴随点为A2,点A2的伴随点为A3,点A3的伴随点为A4,…,这样依次得到点A1,A2,A3,…,An,….若点A1的坐标为(2,4),点A2017的坐标为 ( )
A. (-3,3) B. (-2,-2) C. (3,-1) D. (2,4)
科目:初中数学 来源: 题型:
【题目】如果关于x的一元二次方程ax2+bx+c=0有两个实数根,且其中一个根为另一个根的3倍,则称这样的方程为“立根方程”.以下关于立根方程的说法:
①方程x2﹣4x﹣12=0是立根方程;
②若点(p,q)在反比例函数y=![]() 的图象上,则关于x的方程px2+4x+q=0是立根方程;
的图象上,则关于x的方程px2+4x+q=0是立根方程;
③若一元二次方程ax2+bx+c=0是立根方程,且相异两点M(1+t,s),N(4﹣t,s)都在抛物线y=ax2+bx+c上,则方程ax2+bx+c=0的其中一个根是![]() .
.
正确的是( )
A. ①② B. ② C. ③ D. ②③
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,长青化工厂与A、B两地有公路、铁路相连.这家工厂从A地购买一批每吨1000元的原料运回工厂,制成每吨8000元的产品运到B地.已知公路运价为1.5元/(吨·千米),铁路运价为1.2元/(吨·千米),且这两次运输共支出公路运输费15000元,铁路运输费97200元.

求:(1)该工厂从A地购买了多少吨原料?制成运往B地的产品多少吨?
(2)这批产品的销售款比原料费与运输费的和多多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
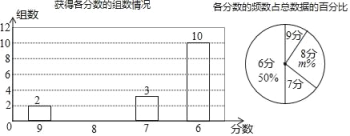
【题目】目前由重庆市教育委员会,渝北区人们政府主办的“阳光下成长”重庆市第八届中小学生艺术展演活动落下帷幕,重庆一中学生舞蹈团、管乐团、民乐团、声乐团、话剧团等五大艺术团均荣获艺术表演类节目一等奖,重庆一中获优秀组织奖,重庆一中老师李珊获先进个人奖,其中重庆一中舞蹈团将代表重庆市参加明年的全国集中展演比赛,若以下两个统计图统计了舞蹈组各代表队的得分情况:
(1)m= ,在扇形统计图中分数为7的圆心角度数为 度.
(2)补全条形统计图,各组得分的中位数是 分,众数是 分.
(3)若舞蹈组获得一等奖的队伍有2组,已知主办方各组的奖项个数是按相同比例设置的,若参加该展演活动的总队伍数共有120组,那么该展演活动共产生了多少个一等奖?
查看答案和解析>>
科目:初中数学 来源: 题型:
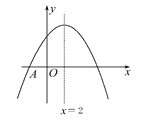
【题目】如图,抛物线y=ax2+bx+c与x轴交于点A(-2,0),顶点坐标为(2,n),与y轴的交点在(0,3),(0,4)之间(包含端点),则下列结论:①当x>6时,y<0;②5a+b>0;③![]() ≤a≤-
≤a≤-![]() ,④4≤n<5中,正确有( )
,④4≤n<5中,正确有( )
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系![]() 中,点
中,点![]() 的坐标为(0,4),线段
的坐标为(0,4),线段![]() 的位置如图所示,其中点
的位置如图所示,其中点![]() 的坐标为(
的坐标为(![]() ,
,![]() ),点
),点![]() 的坐标为(3,
的坐标为(3,![]() ).
).

(1)将线段![]() 平移得到线段
平移得到线段![]() ,其中点
,其中点![]() 的对应点为
的对应点为![]() ,点
,点![]() 的对应点为点
的对应点为点![]() .
.
①点![]() 平移到点
平移到点![]() 的过程可以是:先向 平移 个单位长度,再向 平移 个单位长度;
的过程可以是:先向 平移 个单位长度,再向 平移 个单位长度;
②点![]() 的坐标为 .
的坐标为 .
(2)在(1)的条件下,若点![]() 的坐标为(4,0),连接
的坐标为(4,0),连接![]() ,画出图形并求
,画出图形并求![]() 的面积.
的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
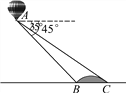
【题目】小明在热气球A上看到正前方横跨河流两岸的大桥BC,并测得B、C两点的俯角分别为45°、35°.已知大桥BC与地面在同一水平面上,其长度为100m,请求出热气球离地面的高度.
(结果保留整数,参考数据:sin35°≈![]() ,cos35°≈
,cos35°≈![]() ,tan35°≈
,tan35°≈![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,在ABCD中,AB=13,BC=50,BC边上的高为12.点P从点B出发,沿B﹣A﹣D﹣A运动,沿B﹣A运动时的速度为每秒13个单位长度,沿A﹣D﹣A运动时的速度为每秒8个单位长度.点Q从点 B出发沿BC方向运动,速度为每秒5个单位长度.P、Q两点同时出发,当点Q到达点C时,P、Q两点同时停止运动.设点P的运动时间为t(秒).连结PQ.
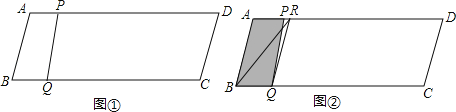
(1)当点P沿A﹣D﹣A运动时,求AP的长(用含t的代数式表示).
(2)连结AQ,在点P沿B﹣A﹣D运动过程中,当点P与点B、点A不重合时,记△APQ的面积为S.求S与t之间的函数关系式.
(3)过点Q作QR∥AB,交AD于点R,连结BR,如图②.在点P沿B﹣A﹣D运动过程中,当线段PQ扫过的图形(阴影部分)被线段BR分成面积相等的两部分时t的值.
(4)设点C、D关于直线PQ的对称点分别为C′、D′,直接写出C′D′∥BC时t的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com