
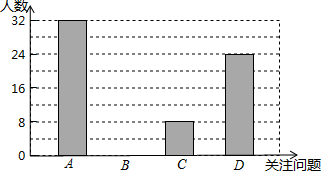
 6��5�������绷���գ�2017�����绷�����й��������ǡ���ˮ��ɽ���ǽ�ɽ��ɽ����С������ѧϰ�������������ĸ����棨A-������Ⱦ��B-��ˮ��ԴΣ����C-���ػ�Į����D-ȫ���ů����ȫУͬѧ����������������飬�˽����������ĸ����������ע�����⣨ÿ����ѡһ��������������²�������ͳ��ͼ����
6��5�������绷���գ�2017�����绷�����й��������ǡ���ˮ��ɽ���ǽ�ɽ��ɽ����С������ѧϰ�������������ĸ����棨A-������Ⱦ��B-��ˮ��ԴΣ����C-���ػ�Į����D-ȫ���ů����ȫУͬѧ����������������飬�˽����������ĸ����������ע�����⣨ÿ����ѡһ��������������²�������ͳ��ͼ����| ��ע������ | Ƶ�� | Ƶ�� |
| A | 32 | m |
| B | a | 0.2 |
| C | 8 | 0.1 |
| D | 24 | n |
| �ϼ� | b | 1 |
���� ��1������C�������Ƶ������Ƶ�ʿɵ�������b������Ƶ��=$\frac{Ƶ��}{����}$�ɵ�n��ֵ��
��2��������������B�������Ƶ�����a��ֵ���ɲ�ȫ����ͼ��
��3�������������A�������Ƶ�ʣ���������������Ƶ�ʿɵô𰸣�
��� �⣺��1�����ε����������b=8��0.1=80���ˣ���
��n=24��80=0.3��
�ʴ�Ϊ��80��0.3��
��2��a=80��0.2=16��
��ȫͼ�����£�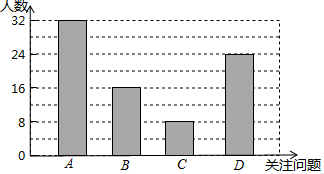
��3����m=32��80=0.4��
��1100��0.4=440��
�𣺸���С���ṩ����Ϣ���Ƹ�У��ע��������Ⱦ����ѧ����Լ��440�ˣ�
���� ���⿼��������ͳ��ͼ��Ƶ�����ʣ��ֲ������Լ��������������壬����ͳ��ͼ������ͳ��ͼ���л�ȡ������Ϣ�ǽ���Ĺؼ���


 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 3 | B�� | 2 | C�� | 1 | D�� | 0 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
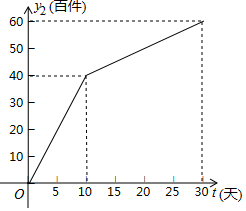 ��������������˾������һ���ļ���װ��ͨ��ʵ���̵�������̵�����;���������ۣ�����һ��ʱ��ù�˾��������Ʒ�����������������Ϊ��30��ĸ��ٵ��飬����ʵ���̵����������y1���ټ�����ʱ��t��tΪ��������λ���죩�IJ��ֶ�Ӧֵ�����ʾ�������̵����������y2���ټ�����ʱ��t��tΪ��������λ���죩�IJ��ֶ�Ӧֵ��ͼ��ʾ��
��������������˾������һ���ļ���װ��ͨ��ʵ���̵�������̵�����;���������ۣ�����һ��ʱ��ù�˾��������Ʒ�����������������Ϊ��30��ĸ��ٵ��飬����ʵ���̵����������y1���ټ�����ʱ��t��tΪ��������λ���죩�IJ��ֶ�Ӧֵ�����ʾ�������̵����������y2���ټ�����ʱ��t��tΪ��������λ���죩�IJ��ֶ�Ӧֵ��ͼ��ʾ��| ʱ��t���죩 | 0 | 5 | 10 | 15 | 20 | 25 | 30 |
| �������� y1���ټ��� | 0 | 25 | 40 | 45 | 40 | 25 | 0 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com