
| A. | (2,3) | B. | (-3,2) | C. | (-2,3) | D. | (3,-2) |
分析 设点P(3,2)关于直线y=x的对称点P′(m,n),由PP′的中点在直线y=x上且直线PP′与直线y=x垂直得到关于m、n的方程组,解之可得答案.
解答 解:设点P(3,2)关于直线y=x的对称点P′(m,n),
∴PP′的中点坐标为($\frac{m+3}{2}$,$\frac{n+2}{2}$),
则中点($\frac{m+3}{2}$,$\frac{n+2}{2}$)在直线y=x上,
∴$\frac{m+3}{2}$=$\frac{n+2}{2}$ ①,
由直线PP′与直线y=x垂直,得$\frac{n-2}{m-3}$=-1 ②,
联立①②,得:$\left\{\begin{array}{l}{m=2}\\{n=3}\end{array}\right.$,
则点P(3,2)关于直线y=x的对称点P′坐标为(2,3),
故选:A.
点评 本题主要考查坐标与图形的变化-对称,熟练掌握轴对称的性质及中点公式、两直线垂直的性质是解题的关键.


科目:初中数学 来源: 题型:解答题
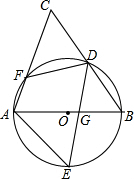 如图,AB是圆O的直径,D、E为圆心O上位于AB异侧的两点,连接BD并延长至点C,连接AC交圆心O于点F,连接AE、DE、DF,已知∠E=∠C.
如图,AB是圆O的直径,D、E为圆心O上位于AB异侧的两点,连接BD并延长至点C,连接AC交圆心O于点F,连接AE、DE、DF,已知∠E=∠C.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
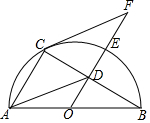 如图,AB是半圆O的直径,D为BC的中点,延长OD交弧BC于点E,点F为OD的延长线上一点且满足∠OBC=∠OFC.
如图,AB是半圆O的直径,D为BC的中点,延长OD交弧BC于点E,点F为OD的延长线上一点且满足∠OBC=∠OFC.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 它的图象分布在第二、四象限 | B. | 它的图象过点(-6,-2) | ||
| C. | 当x<0时,y的值随x的增大而减小 | D. | 与y轴的交点是(0,3) |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
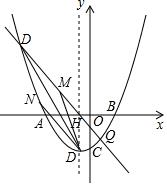 抛物线y=$\frac{1}{3}$x2+bx+c经过点A(-4,0)、B(2,0)两点,与y轴交于点C,顶点为D,对称轴与x轴交于点H,过点H的直线m交抛物线于P、Q两点,其中点P位于第二象限,点Q在y轴的右侧.
抛物线y=$\frac{1}{3}$x2+bx+c经过点A(-4,0)、B(2,0)两点,与y轴交于点C,顶点为D,对称轴与x轴交于点H,过点H的直线m交抛物线于P、Q两点,其中点P位于第二象限,点Q在y轴的右侧.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
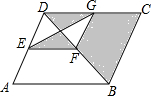 小强喜欢玩飞镖游戏,一天他用平行四边形做了一个飞镖盘,如图所示,?ABCD中,过对角线BD上任一点F分别作FE∥AB,FG∥BC分别交AD,CD于点E,G,连接EG,则小强随机掷一次飞镖,飞镖落在阴影部分的概率是( )
小强喜欢玩飞镖游戏,一天他用平行四边形做了一个飞镖盘,如图所示,?ABCD中,过对角线BD上任一点F分别作FE∥AB,FG∥BC分别交AD,CD于点E,G,连接EG,则小强随机掷一次飞镖,飞镖落在阴影部分的概率是( )| A. | $\frac{1}{4}$ | B. | $\frac{1}{2}$ | C. | $\frac{2}{3}$ | D. | $\frac{3}{5}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com