
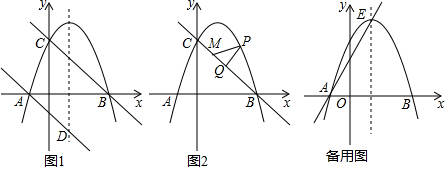
分析 (1)当y=0时,-$\frac{6}{5}$x2+$\frac{4\sqrt{5}}{5}$x+2=0,解方程可得A(-$\frac{\sqrt{5}}{3}$,0),B($\sqrt{5}$,0),当x=0时,y=2,即C(0,2),根据待定系数法可求直线BC的解析式为y=$\frac{2\sqrt{5}}{5}$x+2,根据平行两直线间的关系可得直线AD的解析式为y=-$\frac{2\sqrt{5}}{5}$x-$\frac{2}{3}$,根据抛物线的对称轴为x=-$\frac{b}{2a}$=$\frac{\sqrt{5}}{3}$,可得当x=$\frac{\sqrt{5}}{3}$时,y=-$\frac{2\sqrt{5}}{5}$x-$\frac{2}{3}$=-$\frac{4}{3}$,即D点坐标为($\frac{\sqrt{5}}{3}$,-$\frac{4}{3}$);
(2)如图1,作PF∥y轴交BC于F,则△PQF∽△BOC,根据相似三角形的性质可得PQ=$\frac{\sqrt{5}}{3}$PF,设P(t,-$\frac{6}{5}$t2+$\frac{4\sqrt{5}}{5}$t+2),F(t,$\frac{2\sqrt{5}}{5}$t+2)可得PF=-$\frac{6}{5}$t2+$\frac{6\sqrt{5}}{5}$t,当t=$\frac{\sqrt{5}}{2}$时,PF取最大值,PQ取最大值,此时P($\frac{\sqrt{5}}{2}$,$\frac{5}{2}$),作MN⊥x轴于N,则△BMN∽△BOC,根据相似三角形的性质可得MN=$\frac{2}{3}$BM,则当P,M,N共线时,PM+$\frac{2}{3}$BM=PN=$\frac{5}{2}$,M($\frac{\sqrt{5}}{2}$,1)
(3)如图2所示,分三种情况:1)当A′E′=A′B,A′E′∥BF1,A′E′=BF1时四边形A′E′F1B是菱形;2)当A′E′=E′B,A′E′∥BF2,A′E′=BF2时四边形A′E′F2B是菱形;3)当A′B=E′B,A′F3∥BE′,A′F3=BE′时四边形A′F3E′B是菱形;进行讨论即可求解.
解答 解:(1)当y=0时,-$\frac{6}{5}$x2+$\frac{4\sqrt{5}}{5}$x+2=0,
解得x1=$\sqrt{5}$,x2=-$\frac{\sqrt{5}}{3}$,
即A(-$\frac{\sqrt{5}}{3}$,0),B($\sqrt{5}$,0),
当x=0时,y=2,即C(0,2),
直线BC的解析式为y=-$\frac{2\sqrt{5}}{5}$x+2,
直线AD的解析式为y=-$\frac{2\sqrt{5}}{5}$x-$\frac{2}{3}$,
抛物线的对称轴为x=-$\frac{b}{2a}$=$\frac{\sqrt{5}}{3}$,
当x=$\frac{\sqrt{5}}{3}$时,y=-$\frac{2\sqrt{5}}{5}$x-$\frac{2}{3}$=-$\frac{4}{3}$,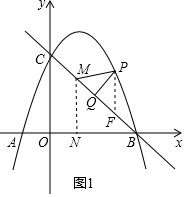 即D点坐标为($\frac{\sqrt{5}}{3}$,-$\frac{4}{3}$);
即D点坐标为($\frac{\sqrt{5}}{3}$,-$\frac{4}{3}$);
(2)如图1,作PF∥y轴交BC于F,
则△PQF∽△BOC,
∴$\frac{PQ}{PF}$=$\frac{BO}{BC}$=$\frac{\sqrt{5}}{3}$
即PQ=$\frac{\sqrt{5}}{3}$PF
设P(t,-$\frac{6}{5}$t2+$\frac{4\sqrt{5}}{5}$t+2),F(t,$\frac{2\sqrt{5}}{5}$t+2)
∴PF=-$\frac{6}{5}$t2+$\frac{6\sqrt{5}}{5}$t
当t=$\frac{\sqrt{5}}{2}$时,PF取最大值,PQ取最大值,
此时P($\frac{\sqrt{5}}{2}$,$\frac{5}{2}$)
作MN⊥x轴于N,则△BMN∽△BOC,
∴$\frac{MN}{BM}$=$\frac{OC}{BC}$=$\frac{2}{3}$
即MN=$\frac{2}{3}$BM,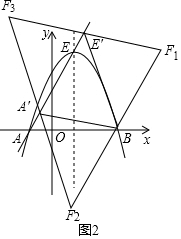 则当P,M,N共线时,PM+$\frac{2}{3}$BM=PN=$\frac{5}{2}$,
则当P,M,N共线时,PM+$\frac{2}{3}$BM=PN=$\frac{5}{2}$,
M($\frac{\sqrt{5}}{2}$,1);
(3)如图2所示,
1)当A′E′=A′B,A′E′∥BF1,A′E′=BF1时四边形A′E′F1B是菱形,
此时A1′($\frac{\sqrt{5}}{3}$,$\frac{8}{3}$),A2′(-$\frac{23\sqrt{5}}{63}$,-$\frac{8}{63}$);
2)当A′E′=E′B,A′E′∥BF2,A′E′=BF2时四边形A′E′F2B是菱形,
此时A3′(-$\frac{\sqrt{5}}{3}$,0),A4′(-$\frac{65\sqrt{5}}{63}$,-$\frac{176}{63}$);
3)当A′B=E′B,A′F3∥BE′,A′F3=BE′时四边形A′F3E′B是菱形,
此时A5′(-$\frac{22\sqrt{5}}{63}$,-$\frac{4}{63}$).
点评 考查了二次函数综合题,涉及的知识点有:待定系数法求一次函数解析式,二次函数的性质,相似三角形的性质,菱形的性质,要会利用数形结合的思想把代数和几何图形结合起来,综合性较强,有一定的难度.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
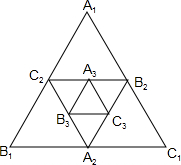 如图,小明作出△A1B1C1,称为第一次操作,分别取△A1B1C1的三边中点A2,B2,C2,作出△A2B2C2,称为第二次操作,用同样的方法,作出△A3B3C3,称为第三次操作,…,第n次操作后,△AnBnCn的面积Sn与△A1B1C1的面积S1之间的数量关系是Sn=$\frac{1}{{4}^{n-1}}$S1.
如图,小明作出△A1B1C1,称为第一次操作,分别取△A1B1C1的三边中点A2,B2,C2,作出△A2B2C2,称为第二次操作,用同样的方法,作出△A3B3C3,称为第三次操作,…,第n次操作后,△AnBnCn的面积Sn与△A1B1C1的面积S1之间的数量关系是Sn=$\frac{1}{{4}^{n-1}}$S1.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 在一年一度的国家学生体质测试中,金星中学对全校2000名男生的1000m测试成绩进行了抽查,学校从初三年级抽取了一部分男生的成绩,并制作成统计表,绘制成频数直方图:
在一年一度的国家学生体质测试中,金星中学对全校2000名男生的1000m测试成绩进行了抽查,学校从初三年级抽取了一部分男生的成绩,并制作成统计表,绘制成频数直方图:| 序号 | 范围(单位:秒) | 频数 | 频率 |
| 1 | 170<x≤200 | 5 | 0.1 |
| 2 | 200<x≤230 | 13 | a |
| 3 | 230<x≤260 | 15 | 0.3 |
| 4 | 260<x≤290 | c | d |
| 5 | 290<x≤320 | 5 | 0.1 |
| 6 | 320<x≤350 | 2 | 0.04 |
| 7 | 350<x≤380 | 2 | 0.04 |
| 合计 | b | 1.00 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com