
【题目】现有一面12米长的墙,某农户计划用28米长的篱笆靠墙围成一个矩形养鸡场ABCD(篱笆只围AB、BC、CD三边),其示意图如图所示.
(1)若矩形养鸡场的面积为92平方米,求所用的墙长AD.(结果精确到0.1米)(参考数据:![]() =1.41,
=1.41,![]() =1.73,
=1.73,![]() =2.24)
=2.24)
(2)求此矩形养鸡场的最大面积.

【答案】(1)所用的墙长AD约为10.5米;(2)矩形养鸡场的最大面积为96平方米
【解析】
(1)直接根据题意表示出矩形的长与宽,再表示出矩形的面积即可得出答案;
(2)利用矩形的长与宽表示出其面积,再根据二次函数的性质即可得出答案.
(1)设AD=x米,则AB=![]() (28﹣x)=(14﹣
(28﹣x)=(14﹣![]() x)米,
x)米,
根据题意,得:x(14﹣![]() x)=92,
x)=92,
解得:x1=14+2![]() ≈17.46>12,不合题意,舍去.
≈17.46>12,不合题意,舍去.
x2=14﹣2![]() =14﹣2×1.73≈10.5,
=14﹣2×1.73≈10.5,
答:所用的墙长AD约为10.5米;
(2)设矩形养鸡场ABCD的面积为S平方米,则:
S=x(14﹣![]() x)=﹣
x)=﹣![]() (x﹣14)2+98,
(x﹣14)2+98,
∵墙长12米,
∴0<x≤12.
∴当x=12时,S取最大值为:﹣![]() (12﹣14)2+98=96,
(12﹣14)2+98=96,
答:此矩形养鸡场的最大面积为96平方米.


 Happy holiday欢乐假期暑假作业广东人民出版社系列答案
Happy holiday欢乐假期暑假作业广东人民出版社系列答案 快乐暑假暑假能力自测中西书局系列答案
快乐暑假暑假能力自测中西书局系列答案科目:初中数学 来源: 题型:
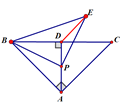
【题目】在Rt△ABC中,∠BAC=90,AB=AC,AD⊥BC于点D,P是线段AD上的一个动点,以点P为直角的顶点,向上作等腰直角三角形PBE,连接DE,若在点P的运动过程中,DE的最小值为3,则AD的长为____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ACB=90°,AC的垂直平分线EF交AC于点D,交AB于点F,且CE=BF.
(1)求证:四边形AECF是菱形;
(2)当∠BAC的度数为多少时,四边形AECF是正方形.

查看答案和解析>>
科目:初中数学 来源: 题型:
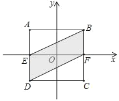
【题目】如图,正方形 ABCD 的对称中心在坐标原点,AB∥x 轴,AD、BC 分别与 x 轴交于 E、F,连接 BE、DF,若正方形 ABCD 的顶点 B,D在双曲线 y ![]() 上,实数 a 满足 a1-a 1,则四边形 DEBF 的面积是_____.
上,实数 a 满足 a1-a 1,则四边形 DEBF 的面积是_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
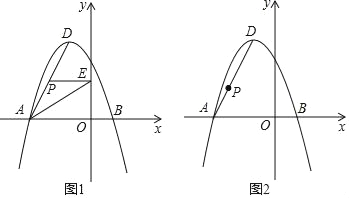
【题目】如图,在平面直角坐标系中,抛物线y=ax2+bx+3经过A(﹣3,0)、B(1,0)两点,其顶点为D,连接AD,点P是线段AD上一个动点(不与A、D重合).
(1)求抛物线的函数解析式,并写出顶点D的坐标;
(2)如图1,过点P作PE⊥y轴于点E.求△PAE面积S的最大值;
(3)如图2,抛物线上是否存在一点Q,使得四边形OAPQ为平行四边形?若存在求出Q点坐标,若不存在请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
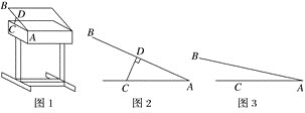
【题目】某课桌生产厂家研究发现,倾斜12°~24°的桌面有利于学生保持躯体自然姿势.根据这一研究,厂家决定将水平桌面做成可调节角度的桌面.新桌面的设计图如图1,AB可绕点A旋转,在点C处安装一根可旋转的支撑臂CD,AC=30 cm.
(1)如图2,当∠BAC=24°时,CD⊥AB,求支撑臂CD的长;
(2)如图3,当∠BAC=12°时,求AD的长.(结果保留根号)
(参考数据:sin 24°≈0.40,cos 24°≈0.91,tan 24°≈0.46,sin 12°≈0.20)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x的一元二次方程:x2﹣(m﹣3)x﹣m=0
(1)证明原方程有两个不相等的实数根;
(2)若抛物线y=x2﹣(m﹣3)x﹣m与x轴交于A(x1,0),B(x2,0)两点,则A,B两点间的距离是否存在最大或最小值?若存在,求出这个值;若不存在,请说明理由.(友情提示:AB=|x1﹣x2|)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com