
【题目】央视热播节目“朗读者”激发了学生的阅读兴趣,某校为满足学生的阅读需求,欲购进一批学生喜欢的图书,学校组织学生会成员随机抽取部分学生进行问卷调查,被调查学生须从“文史类、社科类、小说类、生活类”中选择自己喜欢的一类,根据调查结果绘制了统计图(未完成),请根据图中信息,解答下列问题:
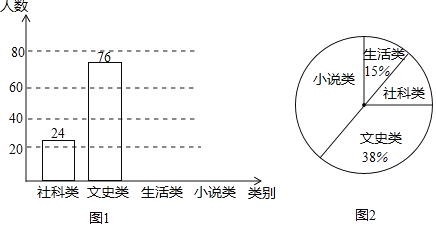
(1)此次共调查了 名学生;
(2)将条形统计图1补充完整;
(3)图2中“小说类”所在扇形的圆心角为 度;
(4)若该校共有学生2000人,估计该校喜欢“社科类”书籍的学生人数.
【答案】(1)200;(2)见解析;(3)126°;(4)240人.
【解析】
(1)根据文史类的人数以及文史类所占的百分比即可求出总人数
(2)根据总人数以及生活类的百分比即可求出生活类的人数以及小说类的人数;
(3)根据小说类的百分比即可求出圆心角的度数;
(4)利用样本中喜欢社科类书籍的百分比来估计总体中的百分比,从而求出喜欢社科类书籍的学生人数
(1)∵喜欢文史类的人数为76人,占总人数的38%,
∴此次调查的总人数为:76÷38%=200人,
故答案为200;
(2)∵喜欢生活类书籍的人数占总人数的15%,
∴喜欢生活类书籍的人数为:200×15%=30人,
∴喜欢小说类书籍的人数为:200﹣24﹣76﹣30=70人,
如图所示:
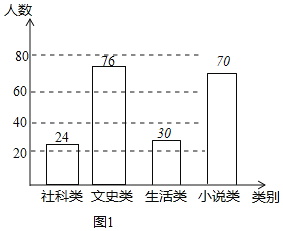
(3)∵喜欢社科类书籍的人数为:24人,
∴喜欢社科类书籍的人数占了总人数的百分比为:![]() ×100%=12%,
×100%=12%,
∴喜欢小说类书籍的人数占了总分数的百分比为:100%﹣15%﹣38%﹣12%=35%,
∴小说类所在圆心角为:360°×35%=126°;
(4)由样本数据可知喜欢“社科类”书籍的学生人数占了总人数的12%,
∴该校共有学生2000人,估计该校喜欢“社科类”书籍的学生人数:2000×12%=240人.


科目:初中数学 来源: 题型:
【题目】为了解我市居民用水情况,在某小区随机抽查了20户家庭,并将这些家庭的月用水量进行统计,结果如下表:
月用水量(吨) | 4 | 5 | 6 | 8 | 13 |
户数 | 4 | 5 | 7 | 3 | 1 |
则关于这20户家庭的月用水量,下列说法正确的是( )
A.中位数是5B.平均数是5C.众数是6D.方差是6
查看答案和解析>>
科目:初中数学 来源: 题型:
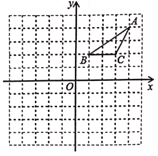
【题目】在正方形网格中建立如图所示的平面直角坐标系![]() ,
,![]() 的三个顶点都在格点上,点
的三个顶点都在格点上,点![]() 的坐标是
的坐标是![]() ,请解答下列问题:
,请解答下列问题:
(1)将![]() 向左平移5个单位长度,画出平移后的
向左平移5个单位长度,画出平移后的![]() ,并写出点
,并写出点![]() 的对应点
的对应点![]() 的坐标;
的坐标;
(2)点![]() 为位似中心,在网格中画出
为位似中心,在网格中画出![]() ,使
,使![]() 与
与![]() 相似,且
相似,且![]() 与
与![]() 的位似比为1:1
的位似比为1:1
(3)![]() (直接写出答案)
(直接写出答案)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD中,M为BC上一点,F是AM的中点,EF⊥AM,垂足为F,交AD的延长线于点E,交DC于点N.

(1)求证:△ABM∽△EFA;
(2)若AB=12,BM=5,求DE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某种小商品的成本价为10元/kg,市场调查发现,该产品每天的销售量w(kg)与销售价x(元/kg)有如下关系w=﹣2x+100,设这种产品每天的销售利润为y(元).
(1)求y与x之间的函数关系式;
(2)当售价定为多少元时,每天的销售利润最大?最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知函数y=![]() (x>0)的图象经过点A、B,点B的坐标为(2,2).过点A作AC⊥x轴,垂足为C,过点B作BD⊥y轴,垂足为D,AC与BD交于点F.一次函数y=ax+b的图象经过点A、D,与x轴的负半轴交于点E
(x>0)的图象经过点A、B,点B的坐标为(2,2).过点A作AC⊥x轴,垂足为C,过点B作BD⊥y轴,垂足为D,AC与BD交于点F.一次函数y=ax+b的图象经过点A、D,与x轴的负半轴交于点E
(1)若AC=![]() OD,求a、b的值;
OD,求a、b的值;
(2)若BC∥AE,求BC的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2016年,淘宝双十一主场狂揽1207亿!你贡献了多少呢?很多老师要剁手,亲,请不要剁手!网上购物已经成为人们常用的一种购物方式,售后评价特别引人关注,如果你感觉买到的东西不好用,就退货,就差评!
作为消费者在网店购买某种商品后,对店家有“好评”、“中评”、“差评”三种评价,假设这三种评价是等可能的.
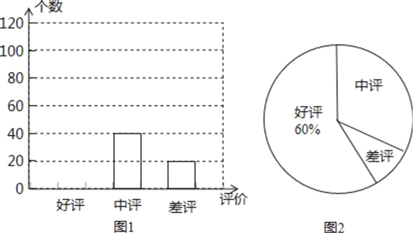
(1)张老师对一家网店销售某种商品显示的评价信息进行了统计,并列出了两幅不完整的统计图.
利用图中所提供的信息解决以下问题:
①张老师一共统计了 个评价;
②请将图1补充完整;
③图2中“差评”所占的百分比是 ;
(2)若甲、乙两名消费者在该网店购买了同一商品,请你用列表格或画树状图的方法帮助店主求一下两人中至少有一个给“好评”的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数![]() (k>0).
(k>0).
(1)当k=![]() 时,求这个二次函数的顶点坐标;
时,求这个二次函数的顶点坐标;
(2)求证:关于x的一元次方程![]() 有两个不相等的实数根;
有两个不相等的实数根;
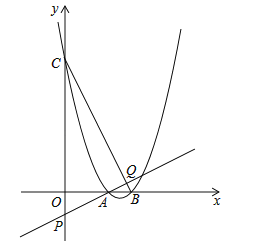
(3)如图,该二次函数与x轴交于A、B两点(A点在B点的左侧),与y轴交于C点,P是y轴负半轴上一点,且OP=1,直线AP交BC于点Q,求证:![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
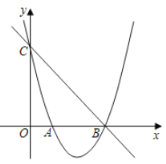
【题目】如图,已知抛物线![]() 经过点
经过点![]() 和点
和点![]() ,与
,与![]() 轴交于点
轴交于点![]() .
.
(1)求此抛物线的解析式;
(2)若点![]() 是直线
是直线![]() 下方的抛物线上一动点(不点
下方的抛物线上一动点(不点![]() ,
,![]() 重合),过点
重合),过点![]() 作
作![]() 轴的平行线交直线
轴的平行线交直线![]() 于点
于点![]() ,设点
,设点![]() 的横坐标为
的横坐标为![]() .
.
①用含![]() 的代数式表示线段
的代数式表示线段![]() 的长;
的长;
②连接![]() ,
,![]() ,求
,求![]() 的面积最大时点
的面积最大时点![]() 的坐标;
的坐标;
(3)设抛物线的对称轴与![]() 交于点
交于点![]() ,点
,点![]() 是抛物线的对称轴上一点,
是抛物线的对称轴上一点,![]() 为
为![]() 轴上一点,是否存在这样的点
轴上一点,是否存在这样的点![]() 和点
和点![]() ,使得以点
,使得以点![]() 、
、![]() 、
、![]() 、
、![]() 为顶点的四边形是菱形?如果存在,请直接写出点
为顶点的四边形是菱形?如果存在,请直接写出点![]() 的坐标;如果不存在,请说明理由.
的坐标;如果不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com