
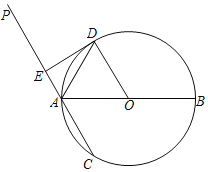
【题目】如图,AB是⊙O的直径,过点A的直线PC交⊙O于A,C两点,AD平分∠PAB,射线AD交⊙O于点D,过点D作DE⊥PA于点E.
(1)求证:ED为⊙O的切线;
(2)若AB=10,ED=2AE,求AC的长.
【答案】(1)ED为⊙O的切线,见解析;(2)6
【解析】
(1)连接AD,根据角平分线的定义得到∠DAE=∠DAO,得到∠ODA=∠DAE,根据平行线的性质得到OD⊥DE,于是得到结论;
(2)过O作OH⊥PC,则四边形EHOD是矩形,求得OH=DE,EH=OD,设AE=x,则DE=2x,根据勾股定理列方程即可得到结论.
解:(1)连接AD,∵AD平分∠PAB,
∴∠DAE=∠DAO,
∵OD=OA,
∴∠ODA=∠OAD,
∴∠ODA=∠DAE,
∴OD∥AE,
∵DE⊥AE,
∴OD⊥DE,
∴ED为⊙O的切线;
(2)过O作OH⊥PC,
则四边形EHOD是矩形,
∴OH=DE,EH=OD,
∵AB=10,
∴EH=OD=5,
∵ED=2AE,
∴设AE=x,则DE=2x,
∴AH=5﹣x,OH=2x,
∵OA2=AH2+OH2,
∴52=(5﹣x)2+(2x)2,
解得:x=2,x=0(不合题意舍去),
∴AE=2,AH=3,
∴AC=6.


 期末金牌卷系列答案
期末金牌卷系列答案 轻松课堂标准练系列答案
轻松课堂标准练系列答案科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,二次函数y=x2+bx+c的图象与x轴交于A、B两点,A点在原点的左侧,B点的坐标为(3,0),与y轴交于点C(0,﹣3).

(1)求二次函数解析式;
(2)若点Q为抛物线上一点,且S△ABQ=![]() S△ACQ,求点Q的坐标;
S△ACQ,求点Q的坐标;
(3)若直线l:y=mx+n与抛物线有两个交点M,N(M在N的左边),P为抛物线上一动点(不与M,N重合).过P作PH平行于y轴交直线l于点H,若![]() =5,求m的值.
=5,求m的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】万州区某民营企业生产的甲、乙两种产品,已知2件甲商品的出厂总价与3件乙商品的出厂总价相同,3件甲商品的出厂总价比2件乙商品的出厂总价多150元.
(1)求甲、乙商品的出厂单价分别是多少元?
(2)为促进万州经济持续健康发展,为商家搭建展示平台,为行业创造交流机会,2019年万州区举办了多场商品展销会.外地一经销商计划购进甲商品200件,购进乙商品的数量是甲的4倍,恰逢展销会期间该企业正在对甲商品进行降价促销活动,甲商品的出厂单价降低了![]() ,该经销商购进甲的数量比原计划增加了
,该经销商购进甲的数量比原计划增加了![]() ,乙的出厂单价没有改变,该经销商购进乙的数量比原计划减少了
,乙的出厂单价没有改变,该经销商购进乙的数量比原计划减少了![]() ,结果该经销商付出的总货款与原计划的总货款恰好相同,求
,结果该经销商付出的总货款与原计划的总货款恰好相同,求![]() 的值
的值![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,点![]() 是原点,四边形
是原点,四边形![]() 是矩形,点
是矩形,点![]() ,点
,点![]() .以点
.以点![]() 为中心,顺时针旋转矩形
为中心,顺时针旋转矩形![]() ,得到矩形
,得到矩形![]() ,点
,点![]() 的对应点分别为
的对应点分别为![]() .
.
(1)如图①,当点![]() 落在
落在![]() 边上时,求点
边上时,求点![]() 的坐标;
的坐标;
(2)如图②,当点![]() 落在线段
落在线段![]() 上时,
上时,![]() 与
与![]() 交于点
交于点![]() .求点
.求点![]() 的坐标;
的坐标;
(3)记![]() 为矩形
为矩形![]() 对角线的交点,
对角线的交点,![]() 为
为![]() 的面积,求
的面积,求![]() 的取值范围(直接写出结果即可).
的取值范围(直接写出结果即可).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,抛物线![]() 交 y轴于点为A,顶点为D,对称轴与x轴交于点H.
交 y轴于点为A,顶点为D,对称轴与x轴交于点H.
(1)求顶点D的坐标(用含m的代数式表示);
(2)当抛物线过点(1,-2),且不经过第一象限时,平移此抛物线到抛物线![]() 的位置,求平移的方向和距离;
的位置,求平移的方向和距离;
(3)当抛物线顶点D在第二象限时,如果∠ADH=∠AHO,求m的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
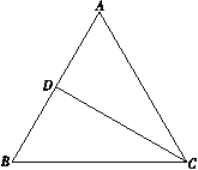
【题目】如图1,在等边三角形ABC中,CD为中线,点Q在线段CD上运动,将线段QA绕点Q顺时针旋转,使得点A的对应点E落在射线BC上,连接BQ,设∠DAQ=α
(0°<α<60°且α≠30°).
(1)当0°<α<30°时,
①在图1中依题意画出图形,并求∠BQE(用含α的式子表示);
②探究线段CE,AC,CQ之间的数量关系,并加以证明;
(2)当30°<α<60°时,直接写出线段CE,AC,CQ之间的数量关系.

![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,如图1,在![]() 中,
中,![]() ,
,![]() ,
,![]() ,若
,若![]() 为
为![]() 的中点,
的中点,![]() 交
交![]() 与点
与点![]() .
.

(1)求![]() 的长.
的长.
(2)如图2,![]() 点为射线
点为射线![]() 上一动点,连接
上一动点,连接![]() ,线段
,线段![]() 绕点
绕点![]() 顺时针旋转
顺时针旋转![]() 交直线
交直线![]() 与点
与点![]() .
.
①若![]() 时,求
时,求![]() 的长:
的长:
②如图3,连接![]() 交直线
交直线![]() 与点
与点![]() ,当
,当![]() 为等腰三角形时,求
为等腰三角形时,求![]() 的长.
的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com