
 如图,已知EF∥AD,∠1=∠2,∠BAC=70°,求∠AGD的度数,下面给出了求∠AGD的度数的过程,将此补充完整并在括号里填写依据.
如图,已知EF∥AD,∠1=∠2,∠BAC=70°,求∠AGD的度数,下面给出了求∠AGD的度数的过程,将此补充完整并在括号里填写依据.分析 先根据平行线的性质以及等量代换,即可得出∠1=∠3,再判定AB∥DG,再根据两直线平行,同旁内角互补,即可得到∠AGD的度数.
解答 解:∵EF∥AD(已知)
∴∠2=∠3(两直线平行,同位角相等)
又∵∠1=∠2(已知)
∴∠1=∠3(等式性质或等量代换)
∴AB∥DG(内错角相等,两直线平行)
∴∠BAC+∠AGD=180°(两直线平行,同旁内角互补)
又∵∠BAC=70°(已知)
∴∠AGD=110°(等式性质)
故答案为:∠3,两直线平行,同位角相等;DG,内错角相等,两直线平行;∠AGD,两直线平行,同旁内角互补.
点评 本题主要考查了平行线的性质与判定的运用,解题时注意:平行线的判定是由角的数量关系判断两直线的位置关系;平行线的性质是由平行关系来寻找角的数量关系.


科目:初中数学 来源: 题型:解答题
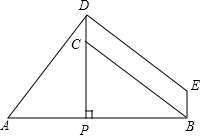 如图,点P在线段AB上,PD⊥AB,点C在线段PD上,连结BC,以CB,CD为邻边构造□BCDE,若AD=DE,AP=PC.
如图,点P在线段AB上,PD⊥AB,点C在线段PD上,连结BC,以CB,CD为邻边构造□BCDE,若AD=DE,AP=PC.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在△ABC中,CD是AB边上的高,CE是∠ACB的平分线.
如图,在△ABC中,CD是AB边上的高,CE是∠ACB的平分线.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com