
【题目】如图,在矩形ABCD中,点F在边BC上,且AF=AD,过点D作DE⊥AF,垂足为点E.
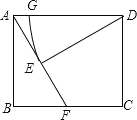
(1)求证:DE=AB.
(2)以D为圆心,DE为半径作圆弧交AD于点G.若BF=FC=1,试求![]() 的长.
的长.
【答案】(1)证明见解析(2)![]()
【解析】
试题分析:(1)由矩形的性质得出∠B=∠C=90°,AB=BC=AD=DC,AD∥BC,得出∠EAD=∠AFB,由AAS证明△ADE≌△FAB,得出对应边相等即可;
(2)连接DF,先证明△DCF≌△ABF,得出DF=AF,再证明△ADF是等边三角形,得出∠DAE=60°,∠ADE=30°,由AE=BF=1,根据三角函数得出DE,由弧长公式即可求出(1)由矩形的性质得出∠B=∠C=90°,AB=BC=AD=DC,AD∥BC,得出∠EAD=∠AFB,由AAS证明△ADE≌△FAB,得出对应边相等即可;
(2)连接DF,先证明△DCF≌△ABF,得出DF=AF,再证明△ADF是等边三角形,得出∠DAE=60°,∠ADE=30°,由AE=BF=1,根据三角函数得出DE,由弧长公式即可求出![]() 的长.
的长.
试题解析:(1)∵四边形ABCD是矩形,
∴∠B=∠C=90°,AB=BC=AD=DC,AD∥BC,
∴∠EAD=∠AFB,
∵DE⊥AF,
∴∠AED=90°,
在△ADE和△FAB中,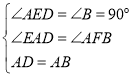 ,
,
∴△ADE≌△FAB(AAS),
∴DE=AB;
(2)连接DF,如图所示:
在△DCF和△ABF中,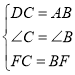 ,
,
∴△DCF≌△ABF(SAS),
∴DF=AF,
∵AF=AD,
∴DF=AF=AD,
∴△ADF是等边三角形,
∴∠DAE=60°,
∵DE⊥AF,
∴∠AED=90°,
∴∠ADE=30°,
∵△ADE≌△FAB,
∴AE=BF=1,
∴DE=![]() AE=
AE=![]() ,
,
∴![]() 的长=
的长=![]() =
=![]() .
.


 海淀课时新作业金榜卷系列答案
海淀课时新作业金榜卷系列答案 期末金牌卷系列答案
期末金牌卷系列答案 轻松课堂标准练系列答案
轻松课堂标准练系列答案科目:初中数学 来源: 题型:
【题目】花粉大小因种而不同,变化很大.最小的花粉是紫草科的勿忘草,直径约为0.0000025米,用科学记数法表示0.0000025为( )
A. 0.25×10﹣5 B. 2. 5×10﹣6 C. 25×10﹣7 D. 2.5×106
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,O为原点,平行四边形ABCD的边BC在x轴上,D点在y轴上,C点坐标为(2,0),BC=6,∠BCD=60°,点E是AB上一点,AE=3EB,⊙P过D,O,C三点,抛物线y=ax2+bx+c过点D,B,C三点.
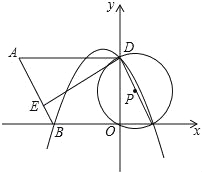
(1)求抛物线的解析式;
(2)求证:ED是⊙P的切线;
(3)若点M为此抛物线的顶点,平面上是否存在点N,使得以点B,D,M,N为顶点的四边形为平行四边形?若存在,请直接写出点N的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC 内一点 P 到三边的距离相等,则点 P 一定是△ABC 的( )
A. 三边垂直平分线的交点B. 三条内角平分线的交点
C. 三条高的交点D. 三条中线的交点
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x的方程(k﹣1)(k﹣2)x2+(k﹣1)x+5=0.
求:(1)当k为何值时,原方程是一元二次方程;
(2)当k为何值时,原方程是一元一次方程,并求出此时方程的解.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com