
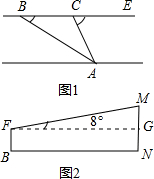
 米到C处,再观察A,此时视线CA与河岸所成的夹角∠ACE=64°.
米到C处,再观察A,此时视线CA与河岸所成的夹角∠ACE=64°. 解:(1)如图,过A作AD⊥BC于D,
解:(1)如图,过A作AD⊥BC于D,| AD |
| tan32° |
| AD |
| tan64° |
| AD |
| tan32° |
| AD |
| tan64° |


科目:初中数学 来源: 题型:
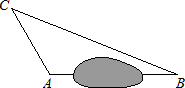 在一次课外实践活动中,同学们要测量某公园人工湖两侧A,B两个凉亭之间的距离.现测得AC=30m,BC=70m,∠CAB=120°,请计算A,B两个凉亭之间的距离.
在一次课外实践活动中,同学们要测量某公园人工湖两侧A,B两个凉亭之间的距离.现测得AC=30m,BC=70m,∠CAB=120°,请计算A,B两个凉亭之间的距离.查看答案和解析>>
科目:初中数学 来源: 题型:
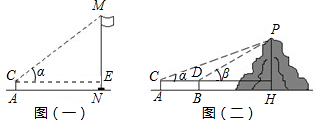
| 题目 | 测量小山的高度 | ||
| 测量数据 |
测量项目 | 测倾器高度 | |
| 仰角α | 20°30′ | 1.2米 | |
| 仰角β | 30° | 小山高度 | |
| AB的距离 | |||
查看答案和解析>>
科目:初中数学 来源: 题型:
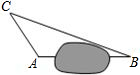 在一次课外实践活动中,同学们要知道校园内A,B两处的距离,但无法直接测得.已知校园内A、B、C三点形成的三角形如图所示,现测得AC=6m,BC=14m,∠CAB=120°,请计算A,B两处之间的距离.
在一次课外实践活动中,同学们要知道校园内A,B两处的距离,但无法直接测得.已知校园内A、B、C三点形成的三角形如图所示,现测得AC=6m,BC=14m,∠CAB=120°,请计算A,B两处之间的距离.查看答案和解析>>
科目:初中数学 来源: 题型:
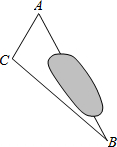 在一次课外实践活动中,同学们要知道校园内A、B两处的距离,但无法直接测得.已知校园内A、B、C三点形成的三角形如图所示,现测得AC=6m,BC=14m,∠CAB=60°,请计算A、B两处之间的距离.
在一次课外实践活动中,同学们要知道校园内A、B两处的距离,但无法直接测得.已知校园内A、B、C三点形成的三角形如图所示,现测得AC=6m,BC=14m,∠CAB=60°,请计算A、B两处之间的距离.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com