
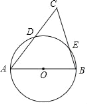
【题目】如图,AB是⊙O的直径,C是⊙O外一点,AC,BC分别与⊙O相交于D.
(1)在图中作出△ABC的边AB上的高CH.(要求:①仅用无刻度真尺,且不能用直尺中的直角;②保留必要的作图痕迹)
(2)连接DE,若![]() ,则∠C的度数是 .
,则∠C的度数是 .
 小学夺冠AB卷系列答案
小学夺冠AB卷系列答案科目:初中数学 来源: 题型:
【题目】![]() 两地相距120km,甲、乙两人从两地出发相向而行,甲先出发.图中
两地相距120km,甲、乙两人从两地出发相向而行,甲先出发.图中![]() 表示两人离
表示两人离![]() 地的距离
地的距离![]() (km)与时间 (h)的关系,结合图像回答下列问题:
(km)与时间 (h)的关系,结合图像回答下列问题:
(1)表示乙离开![]() 地的距离与时间关系的图像是 (填
地的距离与时间关系的图像是 (填![]() 或
或![]() );
);
甲的速度是 km/h,乙的速度是 km/h.
(2)何时两人在途中相遇?
(3)甲出发后多少时间两人恰好相距10km?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,△ABC是等边三角形,D点是AC的中点,延长BC到E,使CE=CD.

(1)用尺规作图的方法,过D点作DM⊥BE,垂足是M(不写作法,保留作图痕迹);
(2)求证:BM=EM.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读理解与应用:对式子x2+2x-3变形如下:x2+2x-3=x2+2x+1-1-3=(x2+2x+1)-4=(x+1)2-4.像这种变形抓住了完全平方公式的特点,先在原式中添加一项,使其中的三项成为完全平方式,再减去添加的这项,我们把这种恒等变形叫配方. 配方法是一种用来把二次多项式化为一个一次多项式的平方与一个常数的和的方法,它的应用十分广泛.请你尝试解决下列问题:
(1)对式子x2-2x+2020进行配方;
(2)已知2y-2x2-8x=y+10,求y的最小值;
(3)如图,在足够大的空地上有一段长为a(a≥250)米的旧墙MN,某人利用旧墙和木栏围成一个长方形菜园ABCD,其中 AD≤MN,已知长方形菜园的一边靠墙,另三边一共用了100米木栏. 求长方形菜园ABCD面积的最大值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某手机店销售一部A型手机比销售一部B型手机获得的利润多50元,销售相同数量的A型手机和B型手机获得的利润分别为3000元和2000元.
(1)求每部A型手机和B型手机的销售利润分别为多少元?
(2)该商店计划一次购进两种型号的手机共110部,其中A型手机的进货量不超过B型手机的2倍.设购进B型手机n部,这110部手机的销售总利润为y元.
①求y关于n的函数关系式;
②该手机店购进A型、B型手机各多少部,才能使销售总利润最大?
(3)实际进货时,厂家对B型手机出厂价下调m(30<m<100)元,且限定商店最多购进B型手机80台.若商店保持两种手机的售价不变,请你根据以上信息及(2)中的条件,设计出使这110部手机销售总利润最大的进货方案.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x的方程x2+(k+3)x+![]() =0有两个不相等的实数根.
=0有两个不相等的实数根.
(1)求k的取值范围;
(2)若方程两根为x1,x2,那么是否存在实数k,使得等式![]() =﹣1成立?若存在,求出k的值;若不存在,请说明理由.
=﹣1成立?若存在,求出k的值;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,点A(0,b),点B(a,0),点D(-2,0),其中a、b满足![]() , DE⊥x轴,且∠BED=∠ABO,直线AE交x轴于点C.
, DE⊥x轴,且∠BED=∠ABO,直线AE交x轴于点C.
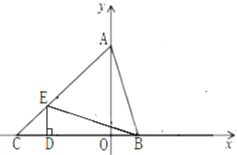
⑴ 分别求出点A、B的坐标;
⑵ 求证:△AOB≌△BDE,并求出点E的坐标
⑶ 若以AB为腰在第一象限内构造等腰直角△ABF,直接写出点F的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读探索
问题背景:著名数学家华罗庚提出把“数形关系”(勾股定理)带到其他星球,作为地球人与其他星球“人”进行第一次”谈话“的语言.2002年8月在北京召开的国际数学大会会标取材于我国古代数学家赵爽的《勾股圆方图注》,它是由四个全等的直角三角形与中间的小正方形拼成的一个大正方形(如图1所示).勾股定理是一条古老的数学定理,它有很多种证明方法,我国汉代数学家赵爽根据弦图,利用面积进行了证明.
赵爽证明方法如下:
以a、b为直角边(b>a),以c为斜边作四个全等的直角三角形,则每个直角三角形的面积等于![]() ,把这四个直角三角形拼成如图1所示形状.
,把这四个直角三角形拼成如图1所示形状.
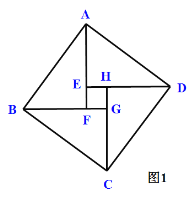
∵Rt△DAE≌Rt△ABF
∴∠EDA=∠FAB
∵∠EAD+∠EDA=90°
∴∠FAB+∠EAD=90°
∴四边形ABCD是一个边长为c的正方形,它的面积等于![]()
∵EF=FG=GH=HE=b-a
∠HEF=90°
∴四边形EFGH是一个边长为b-a的正方形,它的面积等于![]()
∴![]()
∴![]() 从而证明了勾股定理.
从而证明了勾股定理.
思维拓展:
1、如果大正方形的面积为13,小正方形的面积为1,直角三角形的较短直角边长为a,较长直角边长为b,那么![]() 的值为 .
的值为 .
2、美国第二十届总统加菲尔德也曾经给出了勾股定理的一种证明方法,如图2所示,
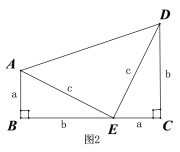
他用两个全等的直角三角形和一个等腰直角三角形拼出了一个直角梯形,请你利用此图形验证勾股定理.
证明:∵直角梯形ABCD的面积可以用两种方法表示:
第一种方法表示为:
第二种方法表示为:
∴ =
∴![]()
探索创新:
用纸做成四个全等的直角三角形,两直角边的长分别为a和b,斜边长为c,请你开动脑筋,将它们拼成一个能证明勾股定理的图形(不同于上面图1和图2).请画出你拼成的图形,并用你画的图形证明勾股定理.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com