
����Ŀ����ͼ1����ƽ��ֱ������ϵ�У�������y=��![]() x2��
x2��![]() x��2
x��2![]() ��x�ύ��A��B���㣨��A�ڵ�B����ࣩ����y���ڵ�C��
��x�ύ��A��B���㣨��A�ڵ�B����ࣩ����y���ڵ�C��
��1����ֱ��AC�Ľ���ʽ��
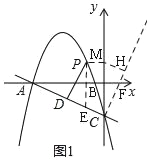
��2����P��ֱ��AC�Ϸ��������ϵ�һ���㣬����P��PD��AC������ΪD�����߶�PD�ij������ʱ����Q�ӵ�P����������ÿ��1����λ���ٶ����ʵ���·���˶���y���ϵĵ�M��������MC��ÿ��3����λ���ٶ��˶�����Cֹͣ������Q�������˶�������ʱ��t����ʱ�����M�����ꣻ
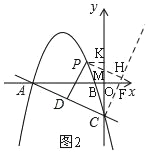
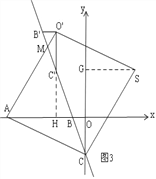
��3����ͼ2������BOC��ֱ��BCƽ�ƣ�ƽ�ƺ�B��O��C����Ķ�Ӧ��ֱ���B�䣬O�䣬C�䣬��S������ƽ����һ�㣬����A��C��O�䣬SΪ������ı��������Σ���ֱ��д�����з��������ĵ�S�����꣮
���𰸡���1��y=��![]() x��2
x��2![]() ����2��M��0��
����2��M��0��![]() ������3����
������3����![]() ��
��![]() ������
������![]() ��
��![]() ����
����![]() ��
��![]() ����
����![]() ��
��![]() ����
����![]() ��
��![]() ��
��
��������������(1)����������ֱ������A�͵�C�����꣬Ȼ�����ô���ϵ���������������ʽ��(2)������P��PE��y�ύֱ��AC�ڵ�E�������P�����꣬�Ӷ��ó�PE�ij��ȣ����ݡ�PDE�͡�AOC���Ƶó�PD�ij��ȣ�Ȼ��֤������CHM����COF���ƣ���PKM����COF���ƣ��Ӷ������M�����ꣻ(3)���������ε����ʷֱ����������������ۣ��ó���P�����꣮
��⣺��1����y=0ʱ����![]() x2��
x2��![]() x��2
x��2![]() =0����������̣��ã�x1=��6��x2=��1��
=0����������̣��ã�x1=��6��x2=��1��
����A����6��0����B����1��0���� ��x=0ʱ��y=��2![]() �� ��C��0����2
�� ��C��0����2![]() ����
����
��ֱ��AC�Ľ���ʽΪ��y=ax+b��a��0����
����A����6��0����C��0����2![]() ������ã�
������ã�![]() �� ��
�� �� ��
��
��ֱ��AC�Ľ���ʽΪ��y=��![]() x��2
x��2![]() ��
��
��2����ͼ1������P��PE��y�ύֱ��AC�ڵ�E��
��P��a����![]()
![]() ��2
��2![]() ����
����
��PE=����![]() ��������
��������![]() ��2
��2![]() ��=��
��=��![]() ��2
��2![]() a��
a��
��AO=6��OC=2![]() �� ��AC=
�� ��AC=![]() =
=![]() =2
=2![]() ��
��
�ߡ�PDE=��AOC=90�㣬��PED=��ACO�� ���PDE�ס�AOC�� ��![]() =
=![]() ��
��
��PD=![]() PE=
PE=![]() =��
=��![]() ��
��![]() �� �Գ����ǣ�a=��3��
�� �Գ����ǣ�a=��3��
�ߩ�![]() ��
��
����a=��3ʱ��PD�ij������ʱ��P������Ϊ����3��2![]() ����
����
��ͼ1��ʾ����x����ȡ��F��1��0��������CF���ӳ���
��CF=![]() =
=![]() =3�� ��sin��OCF=
=3�� ��sin��OCF=![]() =
=![]() ��
��
��M��y����һ�㣬����M��MH��CF�ڵ�H��
����CHM�ס�COF����֪��![]() =
=![]() �� ��t=
�� ��t=![]() =PM+MH��
=PM+MH��
��ͼ2����P��M��H��ͬһֱ����ʱ��t��ֵ��С����ʱ����P��PK��y����K��
����PKM�ס�COF����֪��![]() =2
=2![]() �� ��KM=
�� ��KM=![]() �� ��M��0��
�� ��M��0��![]() ����
����
��3����ͼ3�����ı���ACSO'������ʱ����S��SG��y����G���ӳ�O'C'��x����H��
���ı���ACSO'�����Σ� ��AO'=AC=SC��AO'��SC�� ���AMC=��BCS��
���AO'H+��MC'O'=��BCO+��OCS�� �ߡ�MC'O'=��BCO�� ���AO'H=��OCS��
�ߡ�AHO'=��CGS�� ���O'AH�ա�CSG�� ��AH=SG��O'H=CG��
Rt��OCB��sin��OCB=![]() =
=![]() �� ��sin��BC'H=
�� ��sin��BC'H=![]() =
=![]() ��
��
��BH=x����BC'=3x�� ��C'H=2![]() x�� ��AH=SG=5��x�� ��O'C'=OC=2
x�� ��AH=SG=5��x�� ��O'C'=OC=2![]() ��
��
��C'H=OG=2![]() x�� �ɹ��ɶ����ã�AC2=O'A2�� ��AO2+OC2=O'H2+AH2��
x�� �ɹ��ɶ����ã�AC2=O'A2�� ��AO2+OC2=O'H2+AH2��
��![]() =��5��x��2+��2
=��5��x��2+��2![]() +2
+2![]() x��2�� ��ã�x=
x��2�� ��ã�x=![]() ��
��
��x=![]() ʱ��SG=5��x=
ʱ��SG=5��x=![]() ��OG=2
��OG=2![]() x=
x=![]() ��
��
��x=![]() ��0ʱ�����������⣬��ȥ��SG=5��x=
��0ʱ�����������⣬��ȥ��SG=5��x=![]() ��OG=2
��OG=2![]() x=
x=![]() ��
��
��ʱS������Ϊ��![]() ��
��![]() ��
��
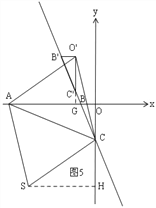
����ͼ4����S��SH��AO��H���ӳ�O'B'��y�ύ��G�� ��SE��CF��EC��SF��
���ı���SECF��ƽ���ı��Σ� ���ESF=��ECF�� ���ı���ASO'C�����Σ�
���ASO'=��ACO'�� ���ASH=��O'CG�� ͬ���ã���ASH�ա�O'CG�� ��AH=O'G��SH=CG��
sin��GCB'=![]() =
=![]() �� ��GB'=x����CB'=3x��CG=2
�� ��GB'=x����CB'=3x��CG=2![]() x�� ��O'G=1+x��
x�� ��O'G=1+x��
�ɹ��ɶ����ã�AC2=O'C2�� ��62+��2![]() ��2=��2
��2=��2![]() x��2+��x+1��2����ã�x=
x��2+��x+1��2����ã�x=![]() ��
��
��x=![]() ʱ��SH=CG=2
ʱ��SH=CG=2![]() x=
x=![]() ��OH=6��AH=6��O'G=5��x=
��OH=6��AH=6��O'G=5��x=![]() ��
��
��x=![]() ��0ʱ�����������⣬��ȥ��
��0ʱ�����������⣬��ȥ��
��ʱ����S������Ϊ����![]() ��
��![]() ����
����
����ͼ5��ACΪ�Խ���ʱ��ͬ���ɵ�S��![]() ��
��![]() ��
��
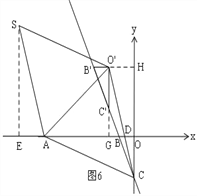
����ͼ6����S��SE��x����E���ӳ�B'O'��y����H���ӳ�O'C'��x����G��
��GB'=x����CB'=3x��CG=2![]() x�� ��O'G=O'H=1+x�� �ߡ�HO'D=��O'DA=��EAS��
x�� ��O'G=O'H=1+x�� �ߡ�HO'D=��O'DA=��EAS��
����SEA�ա�CHO'�� ͬ���ɵ�S��![]() ��
��![]() ����
����
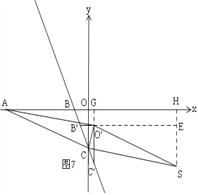
����ͼ7����S��SH��x����H����O'��O'E��SH��E���ӳ�C'O'��x����G��
��OG=x����BG=1+x�� ��O'B'��BG�� ��![]() �� ��
�� ��![]() ��
��
��C'G=2![]() ��1+x���� ��O'G=C'G��C'O'=2
��1+x���� ��O'G=C'G��C'O'=2![]() x�� ��AG=1+x��
x�� ��AG=1+x��
ͬ���ã�62+��2![]() ��2=��1+x��2+��2
��2=��1+x��2+��2![]() x��2��
x��2��
��ã�x1=![]() ��x2=
��x2=![]() ���ᣩ�� �ɵ�S
���ᣩ�� �ɵ�S![]() ��
��
����������S��������![]() ��
��![]() ��
��![]() ��
��![]() ����
����![]() ��
��![]() ����
����![]() ��
��![]() ����
����



 ��У����ϵ�д�
��У����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ijѧУ��չ����ѧ��ʹ���ֻ���������������ȡ����ѧ��������ʹ���ֻ���Ŀ��������ÿ��ʹ���ֻ���ʱ�������ʾ����飬�����Ƴ���ͼ�٣�ͼ�ڵ�ͳ��ͼ����֪������������������40�ˣ�

��1������ε����У�һ����ȡ��������ѧ����
��2��������ͳ��ͼ�У�������Ϸ����Ӧ��Բ�ĽǵĶ����������ȣ�
��3����ȫ����ͳ��ͼ����ע��0-1Сʱ��16�ˣ�
��4����У����ѧ��2660�ˣ������ÿ��ʹ���ֻ�ʱ����2Сʱ���ϣ�����2Сʱ����������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪�����ϵ�A��ʾ����Ϊ6��B��������������һ�㣬��A��B�����ľ���Ϊ10������P�ӵ�A��������ÿ��6����λ���ȵĶ����������������˶������˶�ʱ��Ϊt![]() �롣
�롣
![]()
��1�������ϵ�B��ʾ������______������P�˶���AB���е�ʱ��������ʾ������_____��
��2������Q�ӵ�B��������ÿ��2����λ���ȵ��ٶ����������������˶�������P��Qͬʱ��������
�ٵ���P�˶�������ʱ����P�ϵ�Q��
�ڵ���P�˶�������ʱ����P���Q��ľ���Ϊ8����λ���ȣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�������ݹź�ۡ�ԭ�������غ�ۡ����ųƵ��ۣ����¼��Ϊ��ۣ�����ֲ�����������һǧ�������ʷ����õ����ȡ���Դ������������ﵺ����Ѫ�ȣ����¼����ȣ����������ݸ��ٷ�չ������Ʒ��֮һ��ijˮ�����ϰ���2017��11�·���15200Ԫ������400ǧ�˺�ۺ�600ǧ����ȣ���֪��ȵ�ÿǧ�˽��۱Ⱥ�۵�ÿǧ�˽���2������4Ԫ��
��1����11�·�������ˮ���Ľ��۷ֱ�Ϊÿǧ�˶���Ԫ��
��2��ʱ����ֵ��������������ˮ�����ϰ������12�·ݼ�������������ˮ����������12�·ݣ����ڸ��ٵĴ������У���ۺ���ȵĽ��۶��д���»������ÿǧ�˵Ľ�����11�·ݵĻ������½���![]() m%�����ÿǧ�˵Ľ�����11�·ݵĻ������½���m%�����ں�ۺ͡�õ����ȡ������ܿ�������ӭ��ʵ��ˮ�����ϰ���12�·ݹ����ĺ��������11�·�������
m%�����ÿǧ�˵Ľ�����11�·ݵĻ������½���m%�����ں�ۺ͡�õ����ȡ������ܿ�������ӭ��ʵ��ˮ�����ϰ���12�·ݹ����ĺ��������11�·�������![]() m%����ȹ�����������11�·�������2m%�����12�·��������������ָ��ٵ��ܼ���11�·��������������ָ��ٵ��ܼ���ͬ����m��ֵ��
m%����ȹ�����������11�·�������2m%�����12�·��������������ָ��ٵ��ܼ���11�·��������������ָ��ٵ��ܼ���ͬ����m��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������������ǿѧУ���в��п��Ŵ��Ѽ����ݱ�Ƶ��.Ϊ�����ɸ����������Դ��ѧУ����Ҫ�½�һ��![]() ��Ľ�ѧ��¥��ÿ��¥��
��Ľ�ѧ��¥��ÿ��¥��![]() ����ң������ⶰ��¥����
����ң������ⶰ��¥����![]() ���ţ������������Ŵ�С��ͬ���������Ŵ�С��ͬ����¥ǰΪ�˱�֤ѧ����ȫ����
���ţ������������Ŵ�С��ͬ���������Ŵ�С��ͬ����¥ǰΪ�˱�֤ѧ����ȫ����![]() ���Ž����˲��ԣ���������£���ͬʱ����һ�����ź���������ʱ��
���Ž����˲��ԣ���������£���ͬʱ����һ�����ź���������ʱ��![]() ���ӿ���ͨ��
���ӿ���ͨ��![]() ��ѧ������ͬʱ����һ�����ź�һ������ʱ
��ѧ������ͬʱ����һ�����ź�һ������ʱ![]() ���ӿ���ͨ��
���ӿ���ͨ��![]() ��ѧ��.
��ѧ��.
��1����������£�ƽ��ÿ����һ�����ź�һ�����Ÿ�����ͨ��������ѧ����
��2������з��֣��������ʱ��ѧ��ӵ�������ŵ�Ч�ʽ�����![]() ����ȫ���涨���ڽ��������ȫ��¥��ѧ��Ӧ��
����ȫ���涨���ڽ��������ȫ��¥��ѧ��Ӧ��![]() ������ͨ����
������ͨ����![]() ���Ű�ȫ����.����ⶰ��ѧ¥ÿ��Ԥ������45��ѧ������ô�������
���Ű�ȫ����.����ⶰ��ѧ¥ÿ��Ԥ������45��ѧ������ô�������![]() �����Ƿ���ϰ�ȫ�涨����˵������.
�����Ƿ���ϰ�ȫ�涨����˵������.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������ABCD�У���E��F�ֱ��ڱ�AD��BC�ϣ�EF=2����DEF=60�����ı���EFCD��EF���ۣ��õ��ı���EFC��D����ED����BC�ڵ�G������GEF���ܳ�Ϊ________��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Ϊ��Ӧ���ո�������������������������������������������ijУ��������˲���ѧ������������֪ʶ���������������ѡ���Ϊ��A���dz��˽⣬B���Ƚ��˽�C���˽���٣�D�����˽������֣��������������Ƴ�����������������ͳ��ͼ��
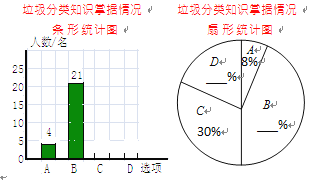
�����ͼ���ṩ����Ϣ������������⣺
(1)������ͳ��ͼ����������
(2)����Уѧ����1000�������ݵ����������Ƹ�У���dz��˽��������Ƚ��˽�����ѧ������________����
(3)��֪���dz��˽�����4��������1��Ů�������������ȡ2����ȫУ�����������֪ʶ���������û���״ͼ���б��ķ�������ǡ�ó鵽1��1Ů�ĸ��ʣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪��������m����ʾ�ĵ㵽��ʾ3�ĵ����4����λ��a��b��Ϊ�෴�����Ҷ���Ϊ�㣬c��d��Ϊ����.
��1����m��ֵ��
��2����![]() ��ֵ.
��ֵ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
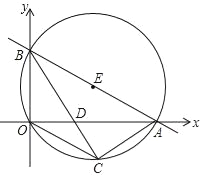
����Ŀ��ֱ��y=��![]() x+
x+![]() �ֱ���x�ᡢy�ύ��A��B���㣬��E����ԭ��O��A��B���㣬C�ǡ�E��һ�㣬����BC��OA�ڵ�D����COD=��CBO��
�ֱ���x�ᡢy�ύ��A��B���㣬��E����ԭ��O��A��B���㣬C�ǡ�E��һ�㣬����BC��OA�ڵ�D����COD=��CBO��
��1����A��B��C�������ꣻ
��2����O��C��A����������߽���ʽ��
��3��ֱ��AB���Ƿ���ڵ�P��ʹ����COP���ܳ���С�������ڣ������P�����ꣻ�������ڣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com