
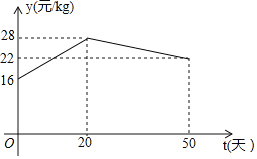
【题目】随着龙虾节的火热举办,某龙虾养殖大户为了发挥技术优势,一次性收购了10000kg小龙虾,计划养殖一段时间后再出售.已知每天养殖龙虾的成本相同,放养10天的总成本为166000,放养30天的总成本为178000元.设这批小龙虾放养t天后的质量为akg,销售单价为y元/kg,根据往年的行情预测,a与t的函数关系为a=![]() ,y与t的函数关系如图所示.
,y与t的函数关系如图所示.
(1)设每天的养殖成本为m元,收购成本为n元,求m与n的值;
(2)求y与t的函数关系式;
(3)如果将这批小龙虾放养t天后一次性出售所得利润为W元.问该龙虾养殖大户将这批小龙虾放养多少天后一次性出售所得利润最大?最大利润是多少?
(总成本=放养总费用+收购成本;利润=销售总额﹣总成本)
【答案】(1)m=600,n=160000;(2)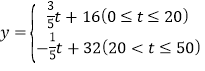 ;(3)该龙虾养殖大户将这批小龙虾放养25天后一次性出售所得利润最大,最大利润是108500元.
;(3)该龙虾养殖大户将这批小龙虾放养25天后一次性出售所得利润最大,最大利润是108500元.
【解析】(1)根据题意列出方程组,求出方程组的解得到m与n的值即可;
(2)根据图象,分类讨论利用待定系数法求出y与P的解析式即可;
(3)根据W=ya﹣mt﹣n,表示出W与t的函数解析式,利用一次函数与二次函数的性质求出所求即可.
(1)依题意得![]() ,
,
解得:![]() ;
;
(2)当0≤t≤20时,设y=k1t+b1,
由图象得:![]() ,
,
解得: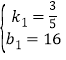
∴y=![]() t+16;
t+16;
当20<t≤50时,设y=k2t+b2,
由图象得:![]() ,
,
解得: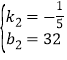 ,
,
∴y=﹣![]() t+32,
t+32,
综上, ;
;
(3)W=ya﹣mt﹣n,
当0≤t≤20时,W=10000(![]() t+16)﹣600t﹣160000=5400t,
t+16)﹣600t﹣160000=5400t,
∵5400>0,
∴当t=20时,W最大=5400×20=108000,
当20<t≤50时,W=(﹣![]() t+32)(100t+8000)﹣600t﹣160000=﹣20t2+1000t+96000=﹣20(t﹣25)2+108500,
t+32)(100t+8000)﹣600t﹣160000=﹣20t2+1000t+96000=﹣20(t﹣25)2+108500,
∵﹣20<0,抛物线开口向下,
∴当t=25,W最大=108500,
∵108500>108000,
∴当t=25时,W取得最大值,该最大值为108500元.


 小题狂做系列答案
小题狂做系列答案科目:初中数学 来源: 题型:
【题目】已知:O是直线AB上的一点,![]() 是直角,OE平分
是直角,OE平分![]() .
.
(1)如图1.若![]() .求
.求![]() 的度数;
的度数;
(2)在图1中,![]() ,直接写出
,直接写出![]() 的度数(用含a的代数式表示);
的度数(用含a的代数式表示);
(3)将图1中的![]() 绕顶点O顺时针旋转至图2的位置,探究
绕顶点O顺时针旋转至图2的位置,探究![]() 和
和![]() 的度数之间的关系.写出你的结论,并说明理由.
的度数之间的关系.写出你的结论,并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场计划购进一批甲、乙两种玩具,已知一件甲种玩具的进价与一件乙种玩具的进价的和为40元,用90元购进甲种玩具的件数与用150元购进的乙种玩具的件数相同.
(1)求每件甲种、乙种玩具的进价分别是多少元?
(2)商场计划购进甲、乙两种玩具共48件,购进这两种玩具的总资金超过960元但不超过1000元,求商场有哪几种具体的进货方案?最多可以购进乙种玩具多少件?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图所示,

(1)作出△ABC关于y轴对称的△A′B′C′,并写出△A′B′C′三个顶点的坐标.
(2)在x轴上画出点P,使PA+PC最小,写出作法.
查看答案和解析>>
科目:初中数学 来源: 题型:
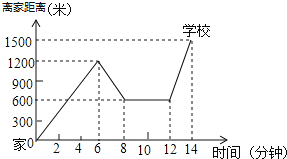
【题目】小明骑单车上学,当他骑了一段路时,想起要买某本书,于是又折回到刚经过的某书店,买到书后继续去学校,以下是他本次上学所用的时间与路程的关系示意图.根据图中提供的信息回答下列问题;
(1)小明家到学校的路程是 米.
(2)小明折回书店时骑车的速度是 米/分,小明在书店停留了 分钟.
(3)本次上学途中,小明一共行驶了 米,从离家至到达学校一共用了 分钟;
(4)在整个上学的途中 分钟至 分钟小明骑车速度最快,最快的速度是 米/分.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在第23个世界读书日前夕,我市某中学为了解本校学生的每周课外阅读时间![]() 用t表示,单位:小时
用t表示,单位:小时![]() ,采用随机抽样的方法进行问卷调查,调查结果按
,采用随机抽样的方法进行问卷调查,调查结果按![]() ,
,![]() ,
,![]() ,
,![]() 分为四个等级,并依次用A,B,C,D表示,根据调查结果统计的数据,绘制成了如图所示的两幅不完整的统计图,由图中给出的信息解答下列问题:
分为四个等级,并依次用A,B,C,D表示,根据调查结果统计的数据,绘制成了如图所示的两幅不完整的统计图,由图中给出的信息解答下列问题:

![]() 求本次调查的学生人数;
求本次调查的学生人数;
![]() 求扇形统计图中等级B所在扇形的圆心角度数,并把条形统计图补充完整;
求扇形统计图中等级B所在扇形的圆心角度数,并把条形统计图补充完整;
![]() 若该校共有学生1200人,试估计每周课外阅读时间满足
若该校共有学生1200人,试估计每周课外阅读时间满足![]() 的人数.
的人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】关于x的方程ax2+bx+c=0(a![]() 0).
0).
(1)已知a,c异号,试说明此方程根的情况.
(2)若该方程的根是x1=-1,x2=3,试求方程a(x+2)2+bx+2b+c=0的根.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com